BFS

La página de BFS está pendiente de mejorar.

BFS es una técnica para recorrer un grafo, a partir de un nodo origen. Proviene de la sigla en inglés “Breadth First Search”, que podríamos traducir aproximadamente como “Buscar primero a lo ancho”. Esta noción da la idea de cómo se recorre el grafo en esta técnica: Se trata de “ir expandiendo” la exploración de los nodos del grafo, en “todas las direcciones a la vez”. De esta forma, el grafo se irá recorriendo en orden de distancia al nodo origen, formandose una suerte de “onda expansiva” a su alrededor:

Por ejemplo, sobre el siguiente grafo:

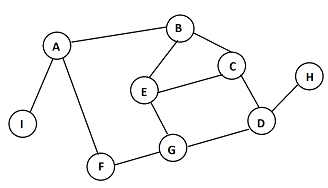
A continuación se muestra el orden en que el algoritmo de BFS irá descubriendo los nodos del grafo, si se comienza una exploración desde el nodo E:

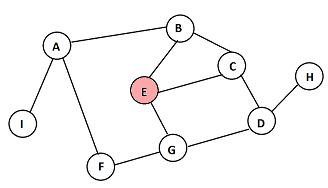
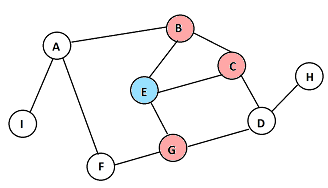
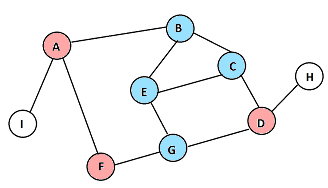
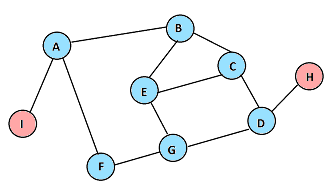
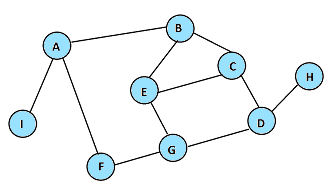
En cada paso, se muestran en rosa los nodos recién descubiertos, y en celeste los que ya habían sido descubiertos en pasos anteriores.

Observando estos ejemplos, es posible caracterizar el mecanismo fundamental del algoritmo de BFS de la siguiente manera:

Se comienza inicialmente con el nodo origen, como único nodo rosa recién descubierto.
La exploración se expande, desde los nodos rosa recién descubiertos, descubriendo nuevos nodos que no habían sido visitados antes. Es decir, todos los nodos blancos (que nunca habían sido vistos) que resultan ser vecinos de los nodos rosa, serán los rosa del próximo paso.
El paso anterior se repite una y otra vez descubriendo más y más nodos en orden, hasta que en algún paso ya no se descubran nodos nuevos. Es decir, se termina el algoritmo cuando ya no hay ningún nodo rosa.

Con esto en mente, podemos dar una implementación del algoritmo. Pero la implementación dependerá necesariamente de la representación que utilicemos.

[pendiente de acomodar, lo que sigue es la explicación clásica que había, que la idea es verla luego de ver la implementación “con bolsas”]

Su implementación es muy sencilla: La lista de nodos que tenemos que mirar será implementada en una queue, que es una estructura de tipo FIFO (First In, First Out, o “el que entra primero sale primero”). La traducción de queue es cola, y da la idea de la cola de un colectivo o de un banco, en la cual la primera persona que llega es la primera en subir o en ser atendida (y eliminada de la cola). Arrancamos con un nodo, y con un arreglo que nos dirá si visitamos el nodo o todavía no. El primero es el único que empieza como que sí. A partir de ahí, mientras nuestra queue tenga “nodos que tenemos que mirar”, agarramos al primero, agregamos a todos sus vecinos que todavía no miramos, y lo sacamos de la lista (implementativamente se suele eliminar primero el nodo que agarramos).

Entonces, si pensamos en las distancias entre el primer nodo y el resto, primero agregamos a todos los de distancia $1$. Luego, para cada uno de estos nodos, agregamos sus vecinos, es decir, los que están a distancia $2$, y así sucesivamente. Por eso “Búsqueda en Anchura”, nos vamos esparciendo hacia lo más alejado pasando por todo lo del medio.

Veamos cómo queda el código, utilizando el recorrido del grafo para saber la distancia desde un nodo dado hasta los demás.

Código

// Tenemos un vector< vector<int> > grafo que en la posición i guarda los vecinos del nodo i
// Tenemos un nodo n inicial a partir del cual nos empezamos a esparcir
int V = grafo.size();
vector <bool> visited(V, false);
vector <int> distancia(V, -1);
queue<int> q;
q.push(n);
visited[n]=true;
distancia[n]=0;
while(!q.empty()){
    int nodoActual = q.front(); // Así miramos al primero de la fila
    q.pop(); // Cuando ya lo guardamos, borramos de la fila al primero
    for(int vecino : grafo[nodoActual]){
        if(visited[vecino]==false){
            q.push(vecino);
            visited[vecino]=true;
            distancia[vecino]=distancia[nodoActual]+1;
        }
    }
}
// En "distancia" quedan guardadas las distancias, y si algún nodo del grafo no está conectado al inicial, es decir que no se puede llegar, distancia guarda un -1.

Complejidad

Se ve que cada vértice se lo mira a lo sumo una vez, y en una visita al nodo se lo agrega/saca de la cola, y se hacen operaciones de tiempo constante, por lo que tenemos $\large O(V)$ tiempo para los vértices. Además, cada arista se ve también a lo sumo una vez, tomando $\large O(E)$ tiempo. En total, la complejidad temporal es $\large O(V+E)$, que en términos de grafos es óptimo.

La complejidad espacial es sencilla de ver. Tenemos el grafo que guarda una entrada por arista (en realidad dos, para la arista $(u,v)$ guarda $v$ en el vector de $u$ y $u$ en el vector de $v$). Luego, los arreglos de visitados y de distancias tienen una variable por nodo, y en la cola a lo sumo están en la cola todos a la vez, una sola vez (si el nodo inicial es vecino de todos). Entonces la complejidad espacial también se ve que es $\large O(V+E)$.

Aplicación interesante: bipartitos

Algo para lo que podemos usar esta técnica de recorrido de grafos, es para ver si podemos pintar los nodos con dos colores, de manera que no haya dos vecinos adyacentes con el mismo color. Otra manera equivalente de decir esto mismo sería: decidir si podemos separar los vértices del grafo en dos conjuntos disjuntos, $V_1$ y $V_2$, de tal forma que todas las aristas del grafo tengan uno de sus extremos en $V_1$ y el otro en $V_2$ ($V_1$ serían los vértices blancos, y $V_2$ los vértices negros).

A los grafos sobre los cuáles se puede realizar lo anterior, se los llama grafos bipartitos. Lo que haríamos sería, comenzar pintando un nodo cualquiera de un color, por ejemplo blanco. Desde ahí, a todos sus vecinos los pintamos de negro. En general, en el mismo BFS de antes, cuando exploramos los vecinos de un cierto nodo, los pintamos con el color contrario al color del nodo actual. Si en algún momento encontramos un nodo que ya está pintado, pero que querríamos pintar del color contrario, entonces en ese caso es imposible pintar con dos colores, y el grafo seguro que no es bipartito. Si el algoritmo termina con todos los nodos pintados, se puede (porque el algoritmo lo logró).

Para facilitar la programación, los colores podemos representarlos simplemente con números. Por ejemplo blanco podría ser $0$, y negro podría ser $1$. De esta forma, si x es un color, su contrario se puede obtener con 1-x, o x^1, o !x.

Una manera equivalente de realizar lo anterior, en lugar de ir pintando con dos colores, es usar el BFS para calcular distancias: en ese caso, los vértices a distancia impar estarán en $V_1$, y los vértices a distancia par estarán en $V_2$ (o viceversa). El grafo será bipartito si y solo si no tiene una arista entre dos vértices que están a una misma distancia del origen.