BFS es una técnica para recorrer un grafo, a partir de un nodo origen. Proviene de la sigla en inglés “Breadth First Search”, que podríamos traducir aproximadamente como “Buscar primero a lo ancho”. Esta noción da la idea de cómo se recorre el grafo en esta técnica: Se trata de “ir expandiendo” la exploración de los nodos del grafo, en “todas las direcciones a la vez”. De esta forma, el grafo se irá recorriendo en orden de distancia al nodo origen, formandose una suerte de “onda expansiva” a su alrededor.

Por ejemplo, sobre el siguiente grafo:

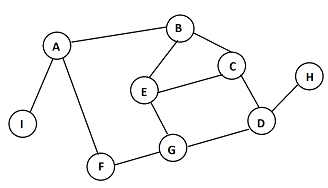
A continuación se muestra el orden en que el algoritmo de BFS irá descubriendo los nodos del grafo, si se comienza una exploración desde el nodo E:

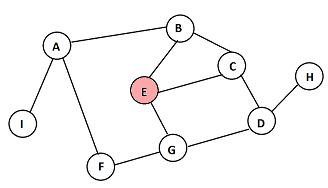
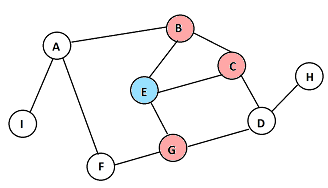
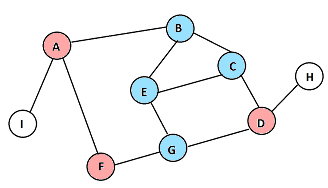
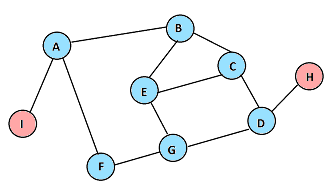
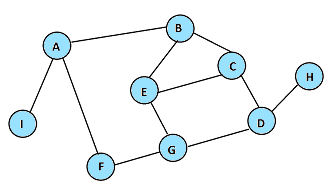
En cada paso, se muestran en rosa los nodos recién descubiertos, y en celeste los que ya habían sido descubiertos en pasos anteriores.

Observando estos ejemplos, es posible caracterizar el mecanismo fundamental del algoritmo de BFS de la siguiente manera:

• Se comienza inicialmente con el nodo origen, como único nodo rosa recién descubierto.
• La exploración se expande, desde los nodos rosa recién descubiertos, descubriendo nuevos nodos que no habían sido visitados antes. Es decir, todos los nodos blancos (que nunca habían sido vistos) que resultan ser vecinos de los nodos rosa, serán los rosa del próximo paso.
• El paso anterior se repite una y otra vez descubriendo más y más nodos en orden, hasta que en algún paso ya no se descubran nodos nuevos. Es decir, se termina el algoritmo cuando ya no hay ningún nodo rosa.

Con esto en mente, podemos dar una implementación del algoritmo. La siguiente implementación asume que los nodos están representados con números de $0$ a $N-1$, que es lo más común, pero las ideas principales no cambian de no ser así.

int origen = 0; // Podria ser otro nodo, se indica aqui
vector<bool> visitado(N, false); // Todos los nodos inician blancos, sin visitar
visitado[origen] = true;
vector<int> rosasActuales = {origen};
while (!rosasActuales.empty())
{
    vector<int> rosasProximos;
    for (int nodo : rosasActuales)
        // ****** para cada vecino de nodo:  ******
            if (!visitado[vecino])
            {
                visitado[vecino] = true;
                rosasProximos.push_back(vecino);
            }
    rosasActuales = rosasProximos;
} 

Como podemos observar, la implementación tiene una parte sin resolver, representada con un comentario: recorrer los vecinos de un nodo dado. La implementación de esa parte dependerá necesariamente de la representación que utilicemos.

Si tenemos el grafo dado como matriz de adyacencia, si $g$ es la matriz de adyacencia (que tiene un 1 en $i,j$ cuando existe arista que va desde $i$ hasta $j$), los vecinos podrían recorrerse de la siguiente manera:

for (int vecino = 0; vecino < n; vecino++)
if (g[nodo][vecino])
{
    ... // Procesar dentro del algoritmo
}

Si el grafo estuviera representado en cambio mediante listas de adyacencia, almacenadas en el arreglo $g$ de manera tal que $g[i]$ es la lista de adyacencia del nodo $i$, el mismo código lo escribiríamos de la siguiente manera:

for (int vecino : g[nodo])
{
    ... // Procesar dentro del algoritmo
}

Si tuvieramos un ejemplo en el cual el grafo fuera un grafo implícito, correspondiente por ejemplo a una grilla con movimientos codificados en arreglos dx y dy, se harían las cuentas correspondientes para obtener y recorrer todos los vecinos.

Como vemos, el único cambio ocurre en la parte del código donde exploramos los vecinos de un nodo: sin importar cómo hayamos resuelto esa parte, todo el resto del algoritmo queda igual.

Si ejecutamos el algoritmo anterior sobre el grafo del ejemplo, empezando con el nodo marcado como $E$, y hacemos que el programa muestre cuáles son los valores contenidos en rosasActuales en cada paso, se obtendría una salida como la siguiente (un paso por línea):

    E 
    B C G 
    A D F 
    I H

Que se corresponde con los dibujos anteriores.

Como comentario final, vale la pena destacar que si bien hemos utilizado fundamentalmente grafos no dirigidos en la explicación, absolutamente todo lo anterior (y todo lo mencionado en este artículo de BFS) funciona perfectamente con grafos dirigidos: el único cuidado que se debe tener es al recorrer los vecinos de un nodo, ya que más que “vecinos” serán “sucesores”: Si la arista es $u \rightarrow v$, debemos considerar $v$ entre los vecinos de $u$, pero no considerar a $u$ entre los vecinos de $v$ (a menos que por supuesto, también haya otra arista $v \rightarrow u$).

Notemos que el orden dentro de cada “bolsa” o “capa” de nodos rosa puede variar dependiendo del orden exacto en el que se vayan recorriendo los vecinos en el algoritmo, pero el orden entre “capas” de la “onda expansiva” no: Primero se recorren todos los nodos a un paso de distancia del origen, en la siguiente bolsa quedan todos los nodos que están a dos aristas de distancia del origen, y así siguiendo.

Esta observación permite utilizar el algoritmo de BFS anterior para calcular las distancias desde el origen hasta todos los demás nodos: La primera capa de “rosasActuales” corresponde a distancia 0 (será únicamente el nodo origen). La segunda corresponde a distancia 1, y así siguiendo. Si se mantiene un contador de distancia que comience en 0, y se incremente luego de cada paso, los nodos de la bolsa de rosasActuales siempre son los que están a la distancia actual indicada por el contador.

A continuación se muestra una modificación a la implementación anterior, que calcula distancias usando la idea que hemos mencionado (con las líneas nuevas indicadas):

int origen = 0;
vector<bool> visitado(N, false);
vector<int> distancia(N, INFINITO); // Linea NUEVA
visitado[origen] = true;
vector<int> rosasActuales = {origen};
int distanciaActual = 0; // Linea NUEVA
while (!rosasActuales.empty())
{
    for (int x : rosasActuales) // Linea NUEVA
        distancia[x] = distanciaActual; // Linea NUEVA
    vector<int> rosasProximos;
    for (int nodo : rosasActuales)
        // ****** para cada vecino de nodo:  ******
            if (!visitado[vecino])
            {
                visitado[vecino] = true;
                rosasProximos.push_back(vecino);
            }
    rosasActuales = rosasProximos;
    distanciaActual++; // Linea NUEVA
} 

Este es un buen momento para mencionar algo que hemos pasado por alto intencionalmente hasta ahora, pero que se relaciona con un detalle del código que acabamos de escribir: la inicialización de las distancias en INFINITO. ¿Por qué hemos hecho eso? Según la definición usual que se usa para la distancia, cuando no existe camino desde un nodo $a$ hasta un nodo $b$, se dice que la distancia $d(a,b) = +\infty$. Lo que hasta ahora venimos asumiendo es que el grafo es conexo. Particularmente, venimos suponiendo que desde el nodo origen es posible alcanzar todos los nodos del grafo, pero esto no tiene por qué ser así. El algoritmo de BFS tiene la propiedad de alcanzar en su expansión a todos aquellos nodos que son alcanzables desde el nodo origen: si existe algún camino desde el origen hasta un cierto nodo $x$, entonces el algoritmo de BFS comenzando en dicho origen, encontrará en algún momento al nodo $x$.

Los nodos que quedan sin encontrar nunca entonces son los no alcanzables, y por lo tanto su distancia es infinito. Con lo cual, es adecuado nuestro valor de inicialización: ponemos todo en infinito, y para aquellos que sean encontrados, la distancia será reemplazada por la distancia verdadera, y quedarán en infinito exactamente los que BFS no recorra, que son aquellos de verdad imposibles de alcanzar.

Si quisiéramos recorrer todo el grafo (por ejemplo, para contar componentes conexas de un grafo no dirigido), lo que podemos hacer generalmente es un for que itere todos los nodos, y cada vez que encuentre un nodo que aún no fue nunca visitado, lance una exploración de BFS nueva con origen en ese nodo, la cual recorrerá todos los alcanzables desde él.

Se suele decir que BFS es un algoritmo “de camino mínimo”, puesto que permite calcular caminos de mínima longitud desde un origen, hasta todos los demás nodos.

Ya hemos visto de hecho cómo calcular las distancias, es decir, las longitudes de esos caminos mínimos. Pero nos faltaría saber cómo calcular los caminos mínimos en sí.

La forma ideal de representar los caminos en BFS es mediante un árbol particular: concretamente, un árbol con raíz en el nodo origen. El árbol así formado es un árbol de caminos mínimos: un camino mínimo desde el origen hasta un nodo cualquiera, se obtendrá (en orden inverso) siguiendo el camino en el árbol desde el nodo objetivo hasta la raíz.

La forma de generar este árbol es manteniendo para cada nodo, su padre en el árbol de caminos mínimos. Este nodo padre será el nodo rosa a través del cuál fue descubierto. Pensemos en términos de las “capas” de distancia de la onda expansiva: un nodo a distancia 2, se descubre (se vuelve un nodo rosa) gracias a que es encontrado al explorar los vecinos de un nodo a distancia 1 (pues una capa descubre la siguiente). Si vamos recorriendo un camino hacia atrás, que siempre baje en uno la distancia al origen, sin dudas el camino en cuestión será mínimo. Eso es lo que se hace al guardar el “padre” de cada nodo: se guarda a qué nodo se debe ir a continuación, para acercarse estrictamente al origen.

De esta manera, una vez completada la ejecución y teniendo todos los padres, para formar el camino desde el origen hasta un cierto nodo, se comienza por el final: a partir del nodo destino, vamos viendo “de dónde se vino”, siguiendo los “padres” en el árbol hasta dar con el comienzo. De esta forma se reconstruye un camino óptimo “marcha atrás”.

A continuación se muestra un árbol de caminos mínimos para el ejemplo anterior (para un recorrido comenzando en el nodo $E$):

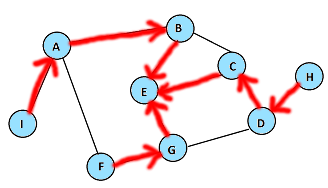
En este caso, este no es el único árbol de caminos mínimos posible: El nodo $D$, que está a distancia 2, se puede descubrir “2 veces” desde la capa anterior: desde el nodo $C$, y desde el nodo $G$. El árbol del ejemplo corresponde al caso en que $C$ ha sido procesado antes que $G$, de manera que $D$ fue marcado como un nodo rosa para el siguiente paso desde $C$, y por lo tanto $C$ queda como padre de $D$ en este caso. Si los vecinos de los nodos se recorrieran en un orden diferente, de tal forma que $G$ fuera procesado primero, el padre de $D$ hubiera sido en su lugar el nodo $G$. Si bien el algoritmo se queda con uno de estos árboles arbitrario, en cualquier caso los caminos obtenidos son óptimos, pues en ambos casos se ve que en “2 saltos” se llega al origen $E$.

Para finalizar, mostramos el código para generar los padres de cada nodo (hemos eliminado en esta versión el cálculo de distancias, pero indudablemente se podría dejar como antes si quisiéramos):

int origen = 0;
vector<bool> visitado(N, false);
vector<int> padre(N, -1); // Linea NUEVA: -1 seria no tener padre: el origen, o los inalcanzables
visitado[origen] = true;
vector<int> rosasActuales = {origen};
while (!rosasActuales.empty())
{
    vector<int> rosasProximos;
    for (int nodo : rosasActuales)
        // ****** para cada vecino de nodo:  ******
            if (!visitado[vecino])
            {
                visitado[vecino] = true;
                rosasProximos.push_back(vecino);
                padre[vecino] = nodo; // Linea NUEVA
            }
    rosasActuales = rosasProximos;
} 

Como se puede apreciar, el mecanismo es sencillísimo: basta agregar una línea cuando se descubre un nodo nuevo, anotando como padre al nodo desde el cuál fue descubierto.

Al final, se puede reconstruir el camino marcha atrás, moviéndose al padre hasta caer en el valor especial “-1”, que hemos usado para indicar que no hay padre.

Suponiendo que explorar los vecinos de un nodo tiene un costo proporcional a su grado (por ejemplo, como ocurre al usar listas de adyacencia), todas estas versiones del algoritmo tienen una complejidad $O(n+m)$.

Esto es porque cada nodo es procesado cuando es rosa, y un nodo es rosa durante únicamente un paso. Por lo tanto, se trabaja con un nodo explorando sus vecinos una única vez en todo el algoritmo. Si explorar los vecinos de un nodo cuesta proporcional a su grado, el costo total del algoritmo, además de un $O(n)$ fijo para crear el arreglo de visitados y similares estructuras, tendrá un costo igual a la suma de todos los grados, que es $2m$. Por lo tanto el total es $O(n+m)$, proporcional al total de nodos y ejes del grafo, lo cual es muy bueno.

Si se utilizara matriz de adyacencia, el costo de buscar los vecinos de un nodo sería siempre $O(n)$, sin importar su grado. En este caso, el costo de explorar cada uno de los $n$ nodos sería siempre $n$, y en total el costo sería $O(n^2)$. Muchas veces es perfectamente razonable un costo de $O(n^2)$, y en estos casos se puede utilizar perfectamente BFS con matriz de adyacencia.

Si bien la idea fundamental del algoritmo de BFS se basa en este recorrido en “capas”, estilo onda expansiva desde un origen, la implementación más común del algoritmo es una que procesa nodo por nodo, sin hacer la “separación en capas” explícitamente. Esta implementación es un poco más corta y más directa, pero es menos evidente el funcionamiento del algoritmo porque la capa actual con la siguiente se encuentran siempre mezcladas en una única cola: esta cola tiene los elementos de la capa actual al comienzo, y los de la capa siguiente van todos al final.

: Revisar y acomodar esta parte, que está escrita menos detalladamente que la anterior

Su implementación es muy sencilla: La lista de nodos que tenemos que mirar será implementada en una queue, que es una estructura de tipo FIFO (First In, First Out, o “el que entra primero sale primero”). La traducción de queue es cola, y da la idea de la cola de un colectivo o de un banco, en la cual la primera persona que llega es la primera en subir o en ser atendida (y eliminada de la cola). Arrancamos con un nodo, y con un arreglo que nos dirá si visitamos el nodo o todavía no. El primero es el único que empieza como que sí. A partir de ahí, mientras nuestra queue tenga “nodos que tenemos que mirar”, agarramos al primero, agregamos a todos sus vecinos que todavía no miramos, y lo sacamos de la lista (implementativamente se suele eliminar primero el nodo que agarramos).

Entonces, si pensamos en las distancias entre el primer nodo y el resto, primero agregamos a todos los de distancia $1$. Luego, para cada uno de estos nodos, agregamos sus vecinos, es decir, los que están a distancia $2$, y así sucesivamente. Por eso “Búsqueda en Anchura”, nos vamos esparciendo hacia lo más alejado pasando por todo lo del medio.

Veamos cómo queda el código, utilizando el recorrido del grafo para saber la distancia desde un nodo dado hasta los demás.

// Tenemos un vector< vector<int> > grafo que en la posición i guarda los vecinos del nodo i
// Tenemos un nodo n inicial a partir del cual nos empezamos a esparcir
int V = grafo.size();
vector <bool> visited(V, false);
vector <int> distancia(V, -1);
queue<int> q;
q.push(n);
visited[n]=true;
distancia[n]=0;
while(!q.empty()){
    int nodoActual = q.front(); // Así miramos al primero de la fila
    q.pop(); // Cuando ya lo guardamos, borramos de la fila al primero
    for(int vecino : grafo[nodoActual]){
        if(visited[vecino]==false){
            q.push(vecino);
            visited[vecino]=true;
            distancia[vecino]=distancia[nodoActual]+1;
        }
    }
}
// En "distancia" quedan guardadas las distancias, y si algún nodo del grafo no está conectado al inicial, es decir que no se puede llegar, distancia guarda un -1.

Se ve que cada vértice se lo mira a lo sumo una vez, y en una visita al nodo se lo agrega/saca de la cola, y se hacen operaciones de tiempo constante, por lo que tenemos $\large O(V)$ tiempo para los vértices. Además, cada arista se ve también a lo sumo una vez, tomando $\large O(E)$ tiempo. En total, la complejidad temporal es $\large O(V+E)$, que en términos de grafos es óptimo.

La complejidad espacial es sencilla de ver. Tenemos el grafo que guarda una entrada por arista (en realidad dos, para la arista $(u,v)$ guarda $v$ en el vector de $u$ y $u$ en el vector de $v$). Luego, los arreglos de visitados y de distancias tienen una variable por nodo, y en la cola a lo sumo están en la cola todos a la vez, una sola vez (si el nodo inicial es vecino de todos). Entonces la complejidad espacial también se ve que es $\large O(V+E)$.

Algo para lo que podemos usar esta técnica de recorrido de grafos, es para ver si podemos pintar los nodos con dos colores, de manera que no haya dos vecinos adyacentes con el mismo color. Otra manera equivalente de decir esto mismo sería: decidir si podemos separar los vértices del grafo en dos conjuntos disjuntos, $V_1$ y $V_2$, de tal forma que todas las aristas del grafo tengan uno de sus extremos en $V_1$ y el otro en $V_2$ ($V_1$ serían los vértices blancos, y $V_2$ los vértices negros).

A los grafos sobre los cuáles se puede realizar lo anterior, se los llama grafos bipartitos. Lo que haríamos sería, comenzar pintando un nodo cualquiera de un color, por ejemplo blanco. Desde ahí, a todos sus vecinos los pintamos de negro. En general, en el mismo BFS de antes, cuando exploramos los vecinos de un cierto nodo, los pintamos con el color contrario al color del nodo actual. Si en algún momento encontramos un nodo que ya está pintado, pero que querríamos pintar del color contrario, entonces en ese caso es imposible pintar con dos colores, y el grafo seguro que no es bipartito. Si el algoritmo termina con todos los nodos pintados, se puede (porque el algoritmo lo logró).

Para facilitar la programación, los colores podemos representarlos simplemente con números. Por ejemplo blanco podría ser $0$, y negro podría ser $1$. De esta forma, si x es un color, su contrario se puede obtener con 1-x, o x^1, o !x.

Una manera equivalente de realizar lo anterior, en lugar de ir pintando con dos colores, es usar el BFS para calcular distancias: en ese caso, los vértices a distancia impar estarán en $V_1$, y los vértices a distancia par estarán en $V_2$ (o viceversa). El grafo será bipartito si y solo si no tiene una arista entre dos vértices que están a una misma distancia del origen.

Distintas movidas en un tablero y cómo simularlo

Guardar distintos tipos de informacion en cada nodo

Charla de Melanie Sclar durante el Certamen Nacional de OIA 2015, hablando sobre grafos en general, y de BFS en particular:

Video

PDF