Tenemos un arreglo de $N \leq 10^5$ enteros. Nos llegan $Q \leq 10^5$ eventos, que pueden ser de dos tipos: Tipo 1. (Actualización) Nos dan un valor $v$ y una posición $i$ y nos piden cambiar el valor de la posición $i$ del arreglo por el nuevo valor $v$. Tipo 2. (Query de rango) Nos dan dos posiciones $a$ y $b$ y nos preguntan el menor valor del arreglo entre las posiciones $a$ y $b$. * En estos problemas conviene que el rango sea incluyendo a $a$ pero no a $b$, esto nos va a ahorrar muchos $+1$ y $-1$ molestos. Es decir, que el rango sea $[a, b)$. Si el problema no me da rango de este tipo, lo más cómodo es transformarlo a un rango de este tipo apenas los leemos de la entrada así no nos preocupamos más por este detalle.

Por ejemplo, el arreglo inicial puede ser: $[1, 5, 3, 7, 2, -3]$ Nos llega un evento de actualización que actualiza la posición $3$ (recordar que las posiciones las numeramos desde $0$) al valor $-1$. El arreglo queda: $[1, 5, 3, -1, 2, -3]$ En este caso no debemos devolver nada, solo desde ahora tener en cuenta que el valor de la posición cambió para los futuros eventos. Ahora nos llega un evento de query de rango para el rango $[1, 5)$, debemos devolver el valor $-1$ que es el mínimo en el rango que contiene los valores $[5, 3, -1, 2]$. Y así, nos prodrían ir llegando más eventos que cambian valores y preguntan por rangos. No hay ninguna restricción en las cantidades de eventos de cada tipo ni el orden en el que llegan.

La idea es poder resolver ambos tipos de queries en $O(log N)$, para eso usaremos una estructura de datos a la que denominamos segment tree.

El segment tree es escencialmente un árbol binario completo. Un árbol binario completo es un árbol con un nodo raiz y donde cada nodo tiene $2$ hijos o es una hoja. El nivel de un nodo es la distancia a la raiz, estando la raiz en el nivel 0, sus hijos en el nivel 1, los hijos de los nodos de nivel 1 en el nivel 2 y así sucesivamente. Y las hojas están todas en el mismo nivel. En este árbol, cada hoja representa una posición del arreglo del problema, de manera que si dibujamos el árbol por niveles, las hojas quedan ordenadas como las posiciones del arreglo que representan de izquierda a derecha.

Como un árbol binario completo tiene una cantidad de hojas potencia de $2$ pero el arreglo puede ser de cualquier tamaño, conviene extender el arreglo agregando posiciones al final hasta que quede de longitud potencia de $2$. Los valores que le agregamos al arreglo no importan, aunque conviene elegir uno que no moleste con el mínimo como $\infty$. 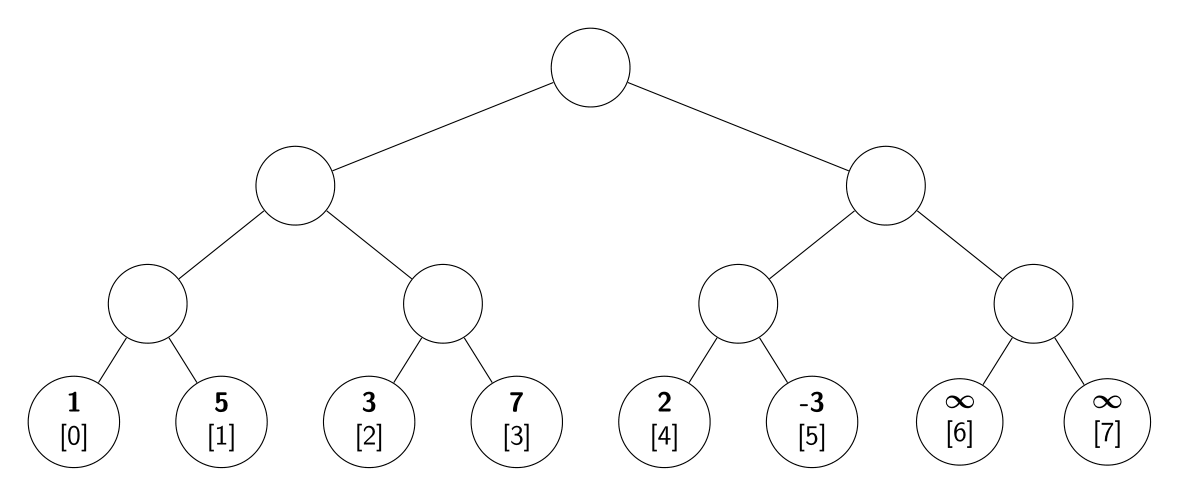Así se ve el árbol para el arreglo inicial del ejemplo ya extendido. En cada hoja tenemos la posición del arreglo que representa y el valor correspondiente en el ejemplo.

Notar que al extender el arreglo hacer esto el tamaño a lo sumo se duplica. Esto nos dice que si procesamos un evento en $O(logN')$ con $N'$ el tamaño del arreglo extendido y $N' < 2N$, entonces $O(logN')$ es $O(logN)$. Por lo que basta probar que podremos procesar las queries en tiempo logaritmico en el tamaño del arreglo extendido. Desde ahora vamos a usar $N$ para el tamaño del arreglo extendido y al remplazar por el $N$ original no cambiarán las complejidades.

* En realidad no hace falta que árbol binario sea completo y se podría modelar de manera que no haya que extender el arreglo, pero es más cómodo trabajar con el árbol completo que posee propiedades buenas como que cada nodo no hoja tiene siempre dos hijos.

Cada nodo no hoja tiene ciertas hojas que cuelgan de él. Todas estas hojas representan un rango de posiciones del arreglo de tamaño potencia de $2$. Este tamaño depende del nivel del nodo, duplicandose a medida que subimos un nivel en el árbol. Un nodo no hoja representará el rango de posiciones de las hojas que cuelgan de él. La idea será guardar en cada nodo del árbol, el resultado de la query de rango para el rango de posiciones que representa el nodo. Si el nodo es una hoja, guardamos el resultado de la query para el rango que contiene la única posición que representa la hoja. Para este problema, en las hojas guardamos los números del arreglo y en los otros nodos guardamos el mínimo de los números de las hojas que cuelgan de él.

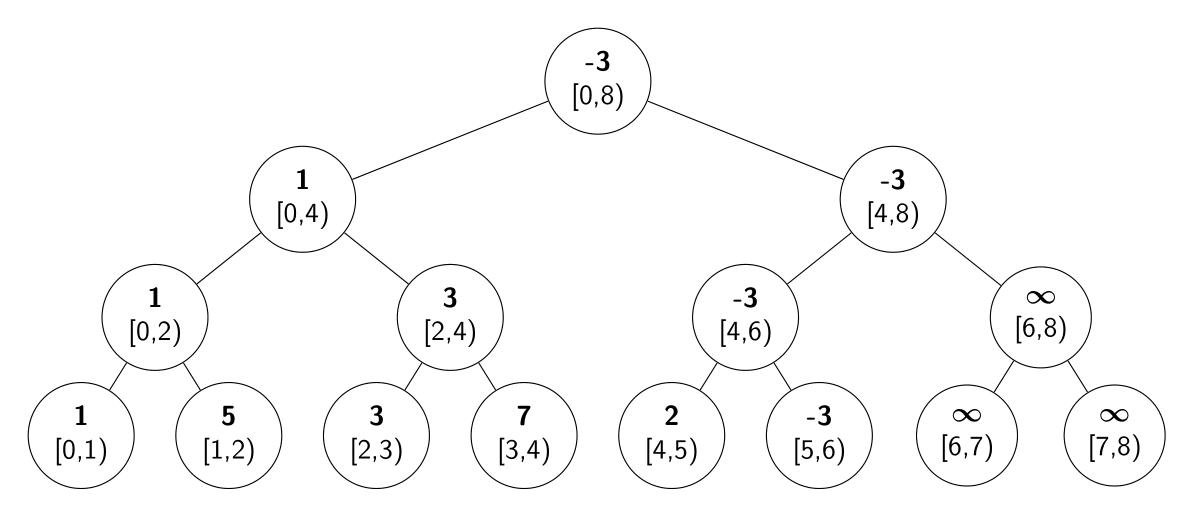Acá vemos como quedarían los valores de los nodos del árbol para el arreglo inicial del ejemplo. Además en cada nodo podemos ver el rango de posiciones que representa.

Esto es todo en cuanto a la estructura del segment tree. Lo que nos queda ver es como resolvemos los distintos eventos de forma eficiente y cómo esta estructura nos ayuda para hacerlo.

Primero que nada, veremos como hacemos para construir el segment tree que corresponde al arreglo inicial. Si bien se puede ver que el algoritmo naive de para cada nodo del árbol recorrer las hojas que le cuelgan y quedarse con el mínimo es $O(nlogn)$, podemos hacer algo mejor. La idea es recorrer los nodos del árbol desde el nivel de abajo (las hojas) hacia arriba. En las hojas simplemente guardamos los valores del arreglo. Luego para cada nodo interno (no hoja) guardamos el mínimo de los valores de sus dos nodos hijos. Si miramos el rango de hojas que cuelgan de un nodo no hoja, la mitad izquierda cuelgan del hijo izquierdo y la mitad derecha del hijo derecho. Luego en el hijo izquierdo tenemos guardado el mínimo de la mitad izquierda del rango y en el derecha tenemos guardado el mínimo de la mitad derecha. Y el mínimo de todo el rango es el mínimo entre el mínimo de la mitad izquierda y la derecha. Al ir llenando de abajo hacia arriba, siempre los dos hijos del nodo ya van a contener el valor correspondiente por lo que podemos calcular el valor de su padre. De esta manera, en $O(1)$ calculamos el valor de cada nodo. Y un árbol binario completo de $N$ hojas tiene $2N-1$ nodos en total. Por lo que inicializamos toods los valores del árbol en $O(2N-1)$ que es $O(N)$.

Cuando llega un evento de actualización que nos pide asignar el valor $v$ a la posición $p$ del arreglo, no nos alcanza con sólo actualizar el arreglo. Tambien queremos que nuestra estructura de segment tree mantenga la propiedad de que cada nodo guarda el valor del mínimo de las hojas que cuelgan de él. Los únicos nodos que pueden llegar a cambiar son los nodos que representan al mínimo de un rango que contiene la posición $p$, es decir, los nodos de los que cuelga la hoja de la posición $p$. Notamos que estos nodos son los nodos del camino de la hoja de la posición $p$ a la raiz. Luego, sólo tenemos que actualizar el valor de estos. Al igual que al inicializar el árbol, podemos hacerlo de abajo hacia arriba facilmente. A la hoja de la posición $p$ le guardamos el nuevo valor $v$ y a medida que subimos por el camino, guardamos en cada nodo el mínimo de sus dos hijos. De esta manera, reestablecemos el invariante del segment tree de que cada nodo contiene el mínimo de su rango correspondiente.

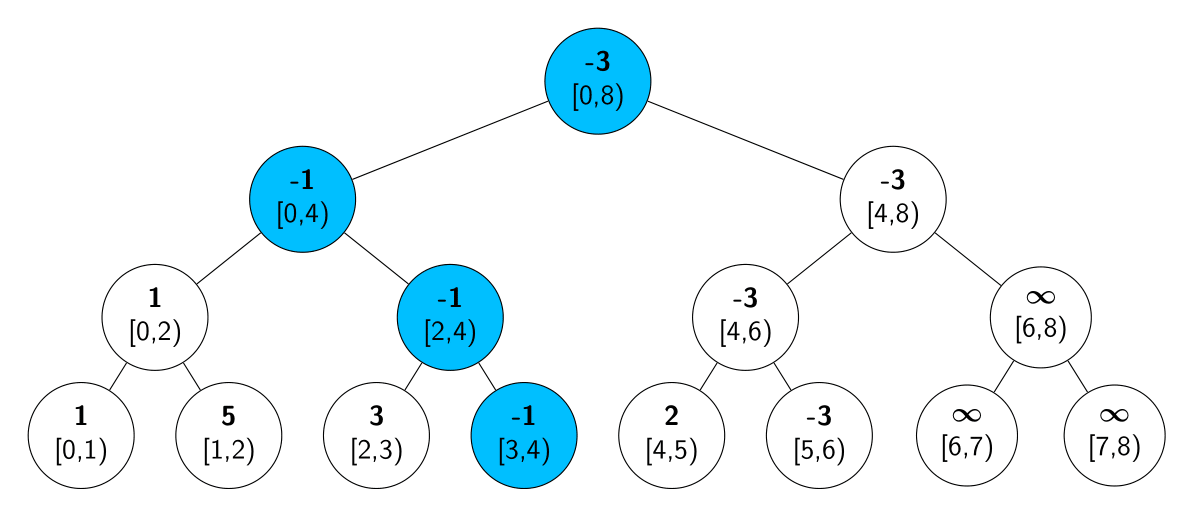Si aplicamos la actualización del ejemplo, que cambia la posición $3$ con el valor $-1$, el árbol queda así. Vemos en azul los nodos con un intervalo que contiene la posición $3$ en los que tuvimos que revisar si hacia falta actualizar su valor. En total tuvimos que actualizar un nodo por nivel, pero un árbol binario completo de $N$ nodos tiene $log(N)+1$ niveles. Por lo que la complejidad de actualizar todo el camino es $O(log N)$ y procesamos el evento en el tiempo que queríamos.

La query de rango es la que a priori no podríamos responder rápido, veamos como gracias a la estructura de segment tree ahora lo podemos hacer. Esta es la parte mas compleja del algoritmo (en términos de dificultad). Supongamos que nos piden el mínimo en el rango $[a, b)$. La idea es encontrar ciertos nodos del árbol que representen rangos que en total cubran todo el intervalo $[a, b)$ (y ningun nodo por fuera de él), luego calculando el mínimo de los valores de todos estos nodos estaríamos obteniendo el mínimo del rango $[a, b)$. Si logramos encontrar estos nodos rápido y la cantidad de estos nodos son del orden de $O(logN)$, lograremos responder la query en $O(logN)$. Para encontrar estos nodos lo que hacemos es ir revisando algunos nodos del árbol empezando de la raiz. Para cada nodo que revisamos tenemos tres casos:

1. Ningun nodo de $[a, b)$ cuelga del nodo. En este caso no nos sirve elegir este nodo ni ninguno de sus hijos ya que no cubren nada del intervalo $[a, b)$. Luego, descartamos este nodo y pasamos al siguiente.
2. Todos los nodos que cuelgan del nodo están en $[a, b)$. En este caso podemos agregar este nodo a la lista de nodos eleigdos y no elegimos ningun hijo de este pues cubren nodos que ya estan quedaron cubiertos con este.
3. Algunos nodos que cuelgan del nodo están en $[a, b)$ y otros no. En este caso, no podemos elegir este nodo pero vamos a tener que elegir algunos de sus hijos para cubrir los nodos de $[a, b)$ que sí cuelgan de este nodo. Lo que hacemos en este caso es agregar a sus dos hijos a la lista de nodos a revisar.

Realizamos este procedimiento hasta que no queden nodos en la lista por revisar y habremos obtenido una lista de nodos que cubren todo el rango $[a, b)$.

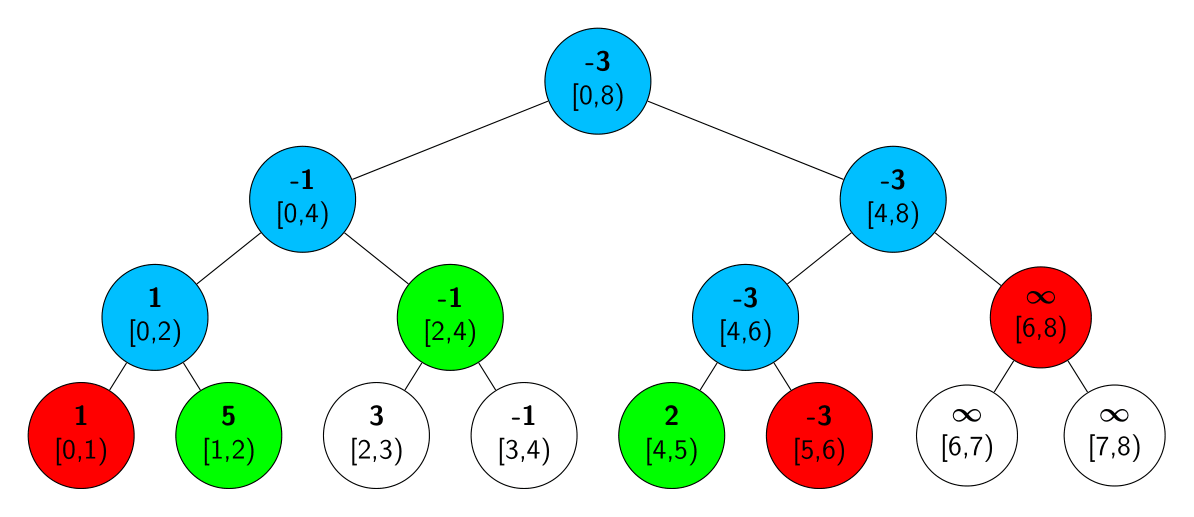
Acá tenemos como queda el algoritmo para la query del ejemplo, donde preguntamos por el rango $[1, 5)$. Los nodos rojos son los que cayeron en el primer caso y fueron descartados. Los nodos verdes son los que cayeron en el segundo caso y fueron los elegidos para cubrir el rango. Los nodos azules son los que cayeron en el tercer caso y revisamos a sus dos hijos. Por último, los nodos blancos son los que no hizo falta revisar.

Queda ver que el algoritmo es lo suficientemente rápido. Si en total revisamos $O(logN)$ nodo, logramos lo que queríamos, ya que la lista de nodos elegidos son algunos de los que revisamos, por lo que tambien son $O(logN)$. La clave para ver que revisamos pocos nodos es ver que por nivel revisamos a lo sumo 4 nodos. Notemos que por cada 2 nodos que revisamos en un nivel, provienen de una nodo del nivel de arriba que cayó en el último caso. Es decir se pueden emparejar de modo que cada par tnega el mismo padre azul. Pero si un nodo cae en último caso (es azul), es porque le cuelgan algunos nodos del rango y otros no. Pero esto sólo puede pasar si le cuelga alguno de los bordes del rango $[a, b)$. Es decir, le cuelga el nodo $a$ o el nodo $b$. Pero por nivel hay un solo nodo del que cuelga el nodo $a$ y uno sólo del que cuelga el nodo $b$ (podrían ser el mismo). Por lo que hay como mucho dos nodos azules por nivel y por lo tanto revisamos a lo sumo 4 nodos por nivel. Luego, en total revisamos a los sumo $4 logN$ nodos que es $O(logN)$ y luego respondemos la query en $O(logN)$.

Si bien es posible implementar el segment tree sobre alguna estructura de grafos o árboles usual, suele ser más cómodo y fácil de implementar directamente guardando los nodos sobre un arreglo. La idea será crear un arreglo $A$ de tamaño $2N$ con $N$ el tamaño del arreglo original ya extendido. Numeramos los nodos del arbol de arriba hacia abajo y de izquierda a derecha, de modo que la raiz es el nodo $1$ y las hojas van del nodo $N$ al $2N-1$. El número de un nodo, representa la posición del arreglo $A$ en donde guardamos el valor del nodo. * Notar que la posición $0$ del arreglo queda sin usar. Hacemos esto para que las cuentas queden más simples más adelante.

Se ve que los hijos de un nodo $i$ son el $2i$ y el $2i+1$ y el padre de el nodo $j$ es el nodo $\lfloor j/2 \rfloor$, es decir la parte entera de $j/2$. Con esta información, ya podemos recorrer el árbol como queramos sin necesidad de guardar las aristas explicitamente.

Lo primero que hacemos es buscar la menor potencia de $2$ mayor a $N$ para saber cuanto extender el arreglo original. Luego guardamos los valores del arreglo original en las posiciones de $N$ a $2N-1$. Por último recorremos de atras para adelante las posiciones de la $1$ a la $N-1$ guardamos el mínimo de los dos hijos como explicamos antes.

vector<int> initSegmentTree(vector<int> arregloInicial) {
    int n = 1;
    while(n < (int) arregloInicial.size()) {
        n *= 2;
    } 
    // Calculamos el tamaño del arreglo extendido
 
    vector<int> segmentTree(2*n, INF);
    for(int i = 0; i < (int) arregloInicial.size(); i++) {
        segmentTree[i+n] = arregloInicial[i];
    } 
    // Llenamos las hojas con los valores del arreglo inicial, las hojas restantes quedan con valor INF
 
    for(int i = n-1; i > 0; i--) {
        segmentTree[i] = min(segmentTree[2*i], segmentTree[2*i+1]);
    }
    // Calculamos los valores de los nodos intermedios
 
    return segmentTree;
}

Como vimos, para actualizar el árbol despues de cambiar el valor de una posición $p$, debemos actualizar los nodos del camino hacia la raiz de abajo hacia arriba. Esto se puede hacer empezando por el nodo que representa la posición $p$ que es el $p+n$ y recorriendo sus padres hasta llegar a la raiz (nodo $1$).

void updateSegmentTree(vector<int>& segmentTree, int posicion, int valor) {
    int n = segmentTree.size()/2;
 
    int nodoActual = posicion+n;
    segmentTree[nodoActual] = valor;
    while(nodoActual > 1) {
        nodoActual /= 2; // Voy al padre
        segmentTree[nodoActual] = min(2*nodoActual, 2*nodoActual+1); // Actualizo
    }
}

Para implementar la query de rango que pregunta por el mínimo en un rango $[a, b)$, vamos a hacer algo similar a lo que explicamos antes, pero implementado de forma recursiva. La idea será que cada nodo devuelva el mínimo de los nodos verdes que cuelgan de él. Esto es equivalente al mínimo entre la intersección entre el rango $[a, b)$ y el rango que representa el nodo. Como del nodo raiz cuelgan todos los nodos verdes (o el rango que representa la raiz es todo el arreglo y la intersección con $[a, b)$ es todo $[a, b)$) la respuesta de la query será el resultado que devuelva el nodo raiz. La recursión hará lo siguiente segun el color del nodo:

1. Para un nodo verde, el resultado es el valor del nodo, ya que todos los hijos de un nodo verde son blancos.
2. Para un nodo rojo, los hijos son todos blancos, por lo que no hay ningun nodo verde que cuelgue de él y el mínimo queda indefinido. Podemos devolver un valor como $\infty$ que no moleste con el mínimo.
3. Para un nodo azul, llamamos recursivamente a sus dos hijos y devolvemos el mínimo de la respuesta de ambos hijos.

Lo que queda es ver eficientemente de qué color es un nodo, para eso debemos saber cual es el rango que representa. Lo más fácil para esto es agregar dos parámetros a la recursión que guarden los extremos que representen al nodo. Cuando llamamos recursivamente a los hijos, los llamamos con la mitad izquierda y la mitad derecha del intervalo segun si llamamos la recursión sobre el hijo izquierdo o el hijo derecho. Una vez que tenemos que el nodo representa un intervalo $[c, d)$,

• Es un nodo verde si $[a, b)$ está todo adentro de $[c, d)$ que pasa si $a \geq c$ y $b \leq d$
• Es un nodo rojo si $[a, b)$ y $[c, d)$ no tienen elementos en común. Esto pasa si $[a, b)$ está todo a la izquierda de $[c, d)$ o $[a, b)$ está todo a la derecha de $[c, d)$. El primer caso ocurre si $b \leq c$ y el segundo si $d \leq a$.
• Es azul si no es ni rojo ni verde.

Con esto ya podemos implementar la query:

int querySegmentTree(vector<int>& segmentTree, int a, int b) {
    int n = segmentTree.size()/2;
    return querySegmentTreeEnNodo(segmentTree, 1, 0, n, a, b);
    // inicio la recursión sobre la raiz (nodo 1) que representa el rango [0, N)
}
 
int querySegmentTreeEnNodo(vector<int>& segmentTree, int nodoActual, int extremoIzq, int extremoDer, int a, int b) {
    if(a >= extremoIzq && b <= extremoDer) {
        // Si estoy en un nodo verde
        return segmentTree[nodoActual];
    }
 
    if(b <= extremoIzq || extremoDer <= a) {
        // Si estoy en un nodo rojo
        return INF;
    }
 
    // Si estoy en un nodo azul
    int puntoMedio = (extremoIzq + extremoDer) / 2;
    return min(querySegmentTreeEnNodo(segmentTree, 2*nodoActual, extremoIzq, puntoMedio, a, b), querySegmentTreeEnNodo(segmentTree, 2*nodoActual+1, puntoMedio, extremoDer, a, b));
}

Hasta ahora siempre abordamos el problema que tiene como query de rango hallar el mínimo para ese rango. Sin embargo, esta estructura no sólo funciona para el mínimo sino para muchos casos más de queries de rango. Si el problema se basa sobre un arreglo al que se le aplican eventos de actualización y queries de rango, ésta estructura suele ser útil. Lo único que necesitamos es que para la query de rango, se pueda calcular facilmente la respuesta para un rango dada la respuesta para dos subrangos que lo forman. Más formalmente, debemos poder dar la respuesta para el rango $[a, c)$ dadas las respuestas para el rango $[a, b)$ y $[b, c)$. Algunos ejemplos de queries de rango que cumplen esta propiedad son: mínimo valor, máximo valor, suma, cualquier operación de bits (AND, OR, XOR).

¿Qué debemos cambiar de la implementación para una operación de rango cualquiera? Como dijimos antes, tenemos que tener una operación que nos permita combinar el resultado de dos rangos que se tocan para obtener el resultado del rango de los dos combinados, a esta operación la podemos llamar el merge de dos intervalos. Luego, basta reemplazar en el código, los lugares que dice “min” por la operación de merge. Algo que tambien tenemos que cambiar es el valor “default” que le dimos al resultado de los nodos rojos. Necesitamos algo que sea un neutro para el merge, es decir, un valor tal que si lo mergeamos con otro valor siempre el resultado es el otro valor. Para el máximo podría ser $-\infty$ y para la suma $0$. Sin embargo, peude pasar que no exista este neutro. En este caso podemos devolver un valor especial “indefinido” para los nodos rojos y tener cuidado para que cuando uno de los hijos de un nodo azul es rojo, devolver siempre el valor del otro hijo.