OIA-Wiki

Este es un algoritmo para conocer todos los números primos hasta un número $n$. La idea consiste en ir recorriendo los números, y marcando los que no son primos. Cuando encontramos un número sin marcar, vamos a marcar a todos sus múltiplos (mayores a sí mismo) como que no son primos, ya que son múltiplos de este. Así por ejemplo tenemos:

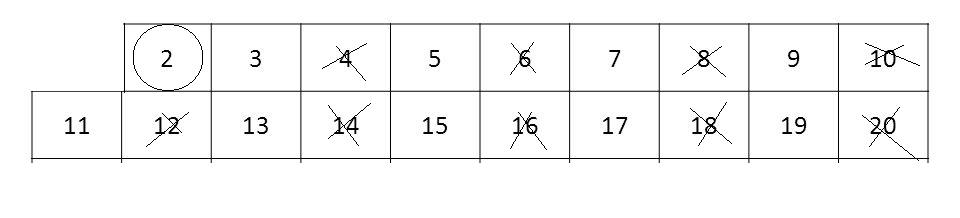
Encontramos que el $2$ está sin marcar, entonces sabemos que es primo y marcamos a sus múltiplos:

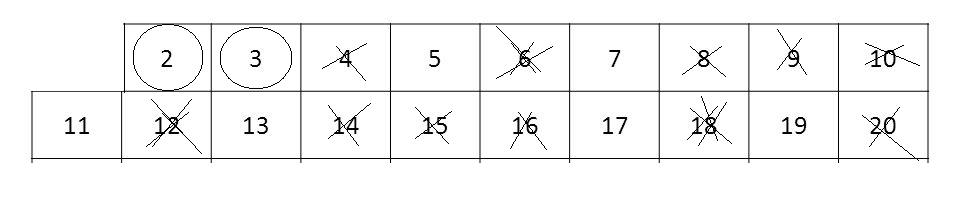
Seguimos y encontramos que el $3$ está sin marcar, y marcamos a sus múltiplos ya que sabemos que no serán primos:

Y así seguimos, encontrando al $5$ y marcando sus múltiplos, al $7$...

criba.cpp

#include<bits/stdc++.h>
 
using namespace std;
 
int main(){
    int N;
    cin>>N;
    vector<int> primes;
    vector<bool> criba(N+1, true); // empiezan todos como "true", posibles primos
    criba[0]=false;
    criba[1]=false;
    for(int i=2; i<=N; i++){
        if(criba[i]){
            primes.push_back(i);
            for(int j=i*2; j<=N; j+=i){
                criba[j]=false;
            }
        }
    }
}

Veamos que para cada número $i$, recorremos (o no) los múltiplos. Es decir, para el número $i$, hacemos $N/i$ iteraciones. Entonces la complejidad quedaría $N/2 + N/3 + N/4 + \ldots N/(N-1) + 1 = N*(1/2 + 1/3 + \ldots) = N*log(N)$. Aunque en realidad, para los números compuestos no entramos al $if$. La complejidad de esta criba (haciendo las cuentas más detalladamente) es $O(N*log(log(N)))$, que es muy cercano a ser lineal, es decir, si $N=10^7$, $log(N)=24$ y $log(log(N))=log(24)=5$.

Algo que podemos ver por ejemplo en la foto, es que al $6$ lo estamos tachando dos veces, ya que es $3*2$. Veamos que cuando estemos en el $5$, vamos a tachar al $10, 15, 20$ que ya estarán tachados. Veamos que en general, al estar en el número $i$, todos los números $i*2, i*3, \ldots, i*(i-1)$ estarán tachados, ya que son compuestos y tienen un divisor (en particular un divisor primo) más chico que $i$. Luego, el $for$ de $j$ podemos empezarlo en $i*i$, que éste sea el primer múltiplo de $i$ que miremos.

A partir de este mejora, podemos pensar entonces que cuando $i*i>N$, el segundo for no haría nada, ya que haríamos $j=i*i$ y la condición de $j \leq N$ se corta sin hacer nada.

Entonces básicamente, si el $for$ de $i$ lo hacemos hasta la raíz de $N$, todos los valores de la criba que nos quedan sin marcar sabemos que serán primos, ya que no tendrán ningún divisor hasta su raíz (que es menor que la raíz de $N$) y como es sabido, esta es la manera de comprobar que es primo.

Ahora, si quisiéramos tener en una lista a todos los primos, sí deberíamos seguir el $for$ de $i$ hasta $N$ e ir agregando los valores en donde $criba[i]$ es $true$. Pero si sólo queremos poder consultar rápidamente si un número es primo o no, alcanza con ir hasta la raíz de $N$, sabiendo que los que quedan en $true$ más adelante son primos.

Podemos ver cómo queda el código con estas mejoras mencionadas:

criba-mejorada.cpp

 
#include<bits/stdc++.h>
 
using namespace std;
 
int main(){
    int N;
    cin>>N;
    vector<int> primes;
    vector<bool> criba(N+1, true);
    criba[0]=false;
    criba[1]=false;
    for(int i=2; i*i<=N; i++){
        if(criba[i]){
            primes.push_back(i);
            for(int j=i*i; j<=N; j+=i){ // si se hace el for de i hasta N, tener cuidado con que i*i se pase del límite de int, usar long long
                criba[j]=false;
            }
        }
    }
    // criba[i] indica verdadero si i es primo y falso si no
}

complejidad

Veamos que en la criba, tenemos una tabla enorme con todos los números hasta el $N$ y sólo guardamos true/false. Qué pasa si guardamos números? Qué números tendría sentido guardar?

Como lo dice el título de la sección, lo que vamos a hacer es guardar factores del número.

Por ejemplo, al recorrer el $2$, guardamos un $2$ en las posiciones por las que pasamos:

Luego, cuando miramos el $3$ (como ya vimos, empezamos desde $3^2$ ya que los múltiplos anteriores ya los vimos):

Entonces cómo factorizar un número?

Bueno, para factorizar $n$, obtenemos de nuestra criba un factor (primo ya que solo insertamos primos como factores) de $n$, $d$. Luego, habrá que factorizar $n/d$, para el cual obtenemos el valor que tiene guardado en la criba. Y así sucesivamente hasta llegar al $1$, momento en el cual paramos. Podemos inicializar a todos l

Veamos cómo queda el código:

criba-para-factorizar.cpp

#include<bits/stdc++.h>
 
using namespace std;
 
int main(){
    int N;
    cin>>N;
    vector<int> criba(N+1, -1);
    for(long long int i=2; i<=N; i++){
        if(criba[i]==-1){
			criba[i]=i;
            for(long long int j=i*i; j<=N; j+=i){
                criba[j]=i;
            }
        }
    }
    for(int i=4; i<=min(N, 20); i++){
		int valor=i;
		vector<int> factores;
		while(valor!=1){
			factores.push_back(criba[valor]);
			valor/=criba[valor];
		}
		sort(factores.begin(), factores.end());
		cout<<"Factores de "<<i<<": ";
		for(int d : factores){
			cout<<d<<", ";
		}
		cout<<endl;
	}
}