En el artículo de búsqueda binaria, que asumimos leído y entendido, se estudian problemas como el lower_bound y otros que trabajan con funciones monótonas. En una función monótona, tanto el problema de buscar el máximo como el mínimo son muy fáciles y poco interesantes: Si la función es creciente, el máximo está en el extremo derecho, y el mínimo en el extremo izquierdo. Si fuera decreciente, sería exactamente al revés.

Otro tipo de función muy importante sobre las cuales es posible calcular muy eficientemente sus valores máximos y mínimos son las funciones unimodales, que es lo que se desarrolla en este artículo.

Una función unimodal¹⁾ es una función de uno de los siguientes dos tipos:

• Unimodal sonriente: función que (al considerar los valores de $x$ de menor a mayor) comienza siendo estrictamente decreciente, luego se mantiene constante, luego es estrictamente creciente. Es decir, se divide el eje $x$ en 3 partes, en las que la función “baja-semantiene-sube”.
• Unimodal triste: análoga a la unimodal sonriente, pero las tres partes son “sube-semantiene-baja”. Es decir, comienza estrictamente creciente, luego se mantiene constante, luego es estrictamente decreciente.

Los nombres de “sonriente” y “triste” se basan en el gráfico de la función, ya que este tendrá la correspondiente “forma de la boca” en un dibujo de “carita triste” o de “carita sonriente”.

La gran utilidad de las funciones unimodales es que se pueden calcular sus valores máximos y mínimos de forma mucho más eficiente que con una búsqueda lineal, algo que no es posible con una función cualquiera que suba y baje todo el tiempo de forma impredecible.

Un ejemplo muy simple de función unimodal sonriente sería el siguiente:

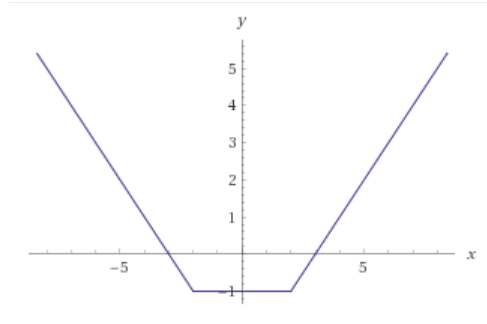
Esta función muy sencilla tiene tres partes, y la función es una recta en cada una: primero baja, luego es horizontal, luego sube, cumpliendo perfectamente lo necesario para ser una función unimodal sonriente.

Otro ejemplo podría ser el siguiente:

En este ejemplo la diferencia entre las partes no es tan evidente en el dibujo, pero se ve que se produce un cambio en el máximo: Allí, la función venía siendo estrictamente creciente, y pasa a ser estrictamente decreciente. En este ejemplo, la parte “constante” del medio tiene longitud $0$. Esto no es un problema, y la función sigue siendo unimodal: lo importante es que, si hay tramos constantes donde ni sube ni baja, estos deben estar todos juntos en el medio, y no en cualquier lugar, o la función no es unimodal. Esta función es unimodal triste.

Los dos ejemplos anteriores fueron funciones convexas y cóncavas respectivamente. Sin embargo, esto no tiene por qué ser así, y hay funciones unimodales que no son ni cóncavas ni convexas. Un ejemplo es la función $f$ dada por $f(x) = x^4 - 2x^2 - 4x$, cuyo gráfico se muestra a continuación:

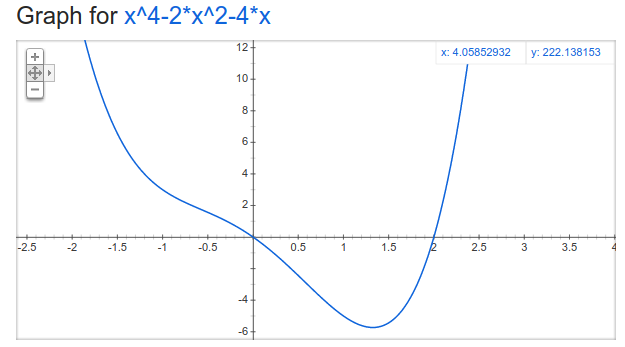
Se puede ver que si bien la función parece “zigzaguear” un poco en su descenso, siempre sigue siendo estrictamente decreciente hasta llegar al valor mínimo, y a partir de allí es siempre estrictamente creciente²⁾. Por lo tanto, esta función es unimodal sonriente, aunque no es convexa.

• El máximo de varias funciones unimodales sonrientes, es también una función unimodal sonriente. Es falso con unimodales tristes.
• El mínimo de varias funciones unimodales tristes, es también una función unimodal triste. Es falso con unimodales sonrientes.
• Una función $f$ es convexa si y solo si $-f$ es cóncava.
• Una función $f$ es unimodal sonriente si y solo si $-f$ es unimodal triste.
• Una función convexa también es automáticamente unimodal sonriente. (Convexa es una condición más fuerte, y las convexas son un tipo especial de unimodales sonrientes).
• Una función cóncava también es automáticamente unimodal triste. (Cóncava es una condición más fuerte, y las cóncavas son un tipo especial de unimodales tristes).
• Las funciones **lineales** son las únicas que son al mismo tiempo convexas y cóncavas.
• Las funciones estrictamente decrecientes, las estrictamente crecientes y las constantes (una recta horizontal horizontal) son las únicas que son al mismo tiempo unimodales tristes y unimodales sonrientes.
• Tanto la suma como el máximo de varias funciones convexas, es a su vez una función convexa.
• Tanto la suma como el mínimo de varias funciones cóncavas, es a su vez una función cóncava.
• CUIDADO: Una suma de funciones unimodales (incluso del mismo tipo) no tiene por qué ser unimodal, a menos que sepamos que además de unimodales también son funciones cóncavas/convexas.

Al final de este artículo se encuentran las ideas para demostrar estas propiedades útiles.

Esta búsqueda tiene la misma idea de base que la búsqueda binaria, sólo que en este caso, la función que vamos a analizar no va ser monótona, sino que la función tendrá dos intervalos disjuntos, en los cuales la función será monótona creciente en uno de los dos, y monótona decreciente en el otro. Estos intervalos deben componer todo el dominio, es decir

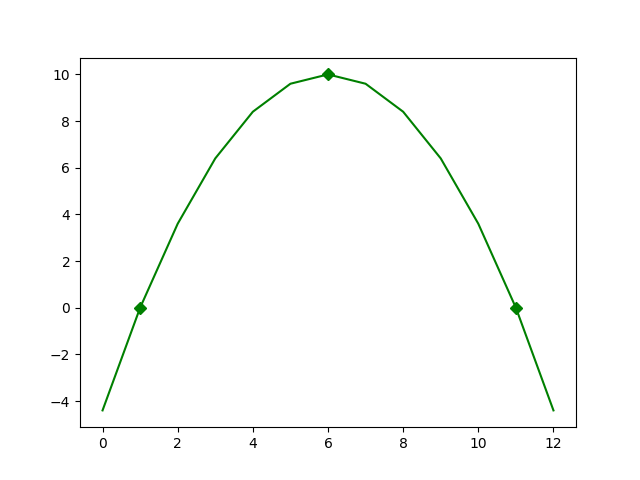
Un esquema típico de una función de este tipo es el siguiente:

Acá, se ve que el valor que divide al dominio en las dos partes es el $6$. Cuando $x < 6$ no se cumple, cuando $x>1$ y $x < 11$ se cumple, y cuando $x \geq 11$ de vuelta no se cumple, la función comienza a decrecer y nunca sube de vuelta.

Dada una función como la de arriba de dominio $[a, b]$, indicar el valor $x$ en el que la función $f(x)$ alcanza su valor máximo.

Empezamos al igual que en la búsqueda binaria, con dos extremos de un intervalo. Los extremos en este caso, serán valores en los cuales sabemos que desde ellos hacia “adentro”, la función no decrece. Es decir sabemos que a la izquierda del extremo izquierdo seguro no está el máximo, y lo mismo a la derecha del extremo derecho. Al principio, estos valores son $l=a$ y $r=b$. A partir de ahí, esta será nuestra invariante: los extremos que tenemos abarcan el máximo. Vamos a correr los extremos todo lo que podemos, y finalmente tendremos que para $x=l=r$ la función alcanza su valor máximo.

Así como antes en la binaria mirábamos un punto intermedio del intervalo, para ver qué extremo correr, ahora mirar un punto no nos dice nada, porque por ejemplo si la función en un punto es más grande que en los extremos, no sabemos si estamos en la primera parte creciendo, o en la segunda parte decreciendo. Entonces vamos a mirar dos valores adentro de nuestro intervalo, $m_1$ y $m_2$, con $m_1<m_2$.

Si $f(m_1) > f(m_2) $, sabemos que ambos puntos están la segunda parte en la que la función decrece, por lo tanto correremos $r=m_2$.

Si $f(m_1) < f(m_2) $, sabemos que estamos en la primera parte donde la función crece, entonces corremos $l=m_1$.

Si $f(m_1)=f(m_2)$, como hay un único valor máximo, sabemos que entre $m_1$ y $m_2$ la función subió y bajó, por lo que efectivamente podemos correr ambos extremos: $l=m_1$ y $r=m_2$.

Para elegir $m_1$ y $m_2$, podemos partir al intervalor [l,r] en tres, y tomar los valores en el primer y segundo tercio, es decir $m_1=l+(r-l)/3$ y $m_2=l+2*(r-l)/3$. Surge un problema cuando $l$ y $r$ están tan cerca que, por ejemplo $(r-l)=2 \Rightarrow (r-l)/3=0$, y entonces $m_1=m_2=l$. Pero bueno, recordemos que en la búsqueda binaria hacíamos $while(r-l>1)$, acá podemos hacer $while(r-l>2)$ para que $(r-l)/3>0$, y luego mirar los tres valores $l, l+1, l+2=r$.

Polo the Penguin and Matrix

Dada una matriz de $n$ x $m$, una movida consiste en sumar o restar el número $d$ a una casilla que elijamos. Determinar la menor cantidad de movidas necesarias para hacer que todos los números sean iguales. Si es imposible, imprimir $-1$.

Para empezar, podemos ver con un poco de matemática, que al sumar o restar $d$ a un número, su resto en la división por $d$ no cambia. Luego, será posible alcanzar el objetivo si y sólo si todos los números tienen el mismo resto en la división por $d$.

Veamos cómo usar búsqueda ternaria en este problema.

Veamos que llevar todos los números a un número muy chiquito, puede llevarnos muchos pasos para mover los números grandes. Lo mismo si queremos llevar todos a un número muy grande, los chiquitos deberían sumar $d$ muchas veces. Entonces tenemos exactamente una función que permite la búsqueda ternaria. Buscaremos un número “intermedio” para el cual sea óptimo llevar a todos los números hacia éste.

Primero hay que ver cómo calcular la cantidad de movidas necesarias para llevar a todos los números a un número $v$, pero eso es fácil: Recorremos todos los números de la matriz, y la cantidad de movidas necesarias para cada número $a$ será la diferencia entre $a$ y $v$, dividido por $d$ que es cuánto se achica esa diferencia en cada movida; es decir, $abs(a-v)/d$.

Sabemos que el menor valor al que intentaremos llevar a todos los números será el valor más chico de la matriz, ya que si llevamos todo a $min-d$ por ejemplo, vamos a pasar por $min$ para todos los números, entonces nos conviene quedarnos ahí y nos llevará más pasos. Lo mismo para el mayor valor.

Hay que tener cuidado porque cuando hagamos (r-l)/3, quizás no caemos en un número de igual resto en la división por $3$ que lo que queremos, entonces pensar en llevar a todos los número hacia éste no tendría sentido. Lo que podemos hacer en este problema para evitar esto, es primero, restarles a todos los números su resto en la división por $d$, total lo que importa son sus diferencias relativas ya que vamos a sumar y restar $d$. Y luego, es pensar “a qué múltiplo de $d$ queremos llevar a todos los números”. Otra manera también sería divir todo por $d$ y pensar que las movidas suman y restan $1$, es completamente equivalente.

solucion-con-ternaria.cpp

#include<bits/stdc++.h>
 
using namespace std;
 
#define forn(i,n) for(int i=0; i<(int)(n); i++)
 
int obtenerMovidas(vector<vector<int> > & matriz, int m, int d){
    int total = 0;
    forn(i, matriz.size()){
        forn(j, matriz[i].size()){
            total+=abs(matriz[i][j]-m)/d;
        }
    }
    return total;
}
 
int main(){
    int n, m, d;
    cin>>n>>m>>d;
    vector< vector<int> > matriz(n, vector<int>(m));
    int restoD;
    bool esPosible=true;
    int minimo=10002, maximo=0;
    forn(i, n){
        forn(j, m){
            cin>>matriz[i][j];
            if(i==0 and j==0){
                restoD=matriz[i][j]%d;
            }else{
                if(restoD!=matriz[i][j]%d){
                    esPosible=false;
                }
            }
            matriz[i][j]-=(matriz[i][j]%d);
            minimo=min(minimo, matriz[i][j]);
            maximo=max(maximo, matriz[i][j]);
        }
    }
    if(esPosible){
        int l=minimo/d, r=maximo/d;
        while(r-l>2){
            int m1=l+(r-l)/3;
            int m2=l+2*(r-l)/3;
            int a=obtenerMovidas(matriz, m1*d, d);
            int b=obtenerMovidas(matriz, m2*d, d);
            if(a<b){ // para m2 necesito mas movidas, no me interesa
                r=m2;
            }else if(a>b){
                l=m1;
            }else{ //a==b
                l=m1;
                r=m2;
            }
        }
        int best=obtenerMovidas(matriz, l*d, d);
        forn(pos, 2){
            best=min(best, obtenerMovidas(matriz, (l+pos+1)*d, d));
        }
        cout<<best<<endl;
    }else{
        cout<<-1<<endl;
    }
}

ternary search en Codeforces

: ¡Escribir unas demos!