En el artículo de búsqueda binaria, que asumimos leído y entendido, se estudian problemas como el lower_bound y otros que trabajan con funciones monótonas. En una función monótona, tanto el problema de buscar el máximo como el mínimo son muy fáciles y poco interesantes: Si la función es creciente, el máximo está en el extremo derecho, y el mínimo en el extremo izquierdo. Si fuera decreciente, sería exactamente al revés.

Otro tipo de función muy importante sobre las cuales es posible calcular muy eficientemente sus valores máximos y mínimos son las funciones unimodales, que es lo que se desarrolla en este artículo.

Una función unimodal¹⁾ es una función de uno de los siguientes dos tipos:

• Unimodal sonriente: función que (al considerar los valores de $x$ de menor a mayor) comienza siendo estrictamente decreciente, luego se mantiene constante, luego es estrictamente creciente. Es decir, se divide el eje $x$ en 3 partes, en las que la función “baja-semantiene-sube”.
• Unimodal triste: análoga a la unimodal sonriente, pero las tres partes son “sube-semantiene-baja”. Es decir, comienza estrictamente creciente, luego se mantiene constante, luego es estrictamente decreciente.

Los nombres de “sonriente” y “triste” se basan en el gráfico de la función, ya que este tendrá la correspondiente “forma de la boca” en un dibujo de “carita triste” o de “carita sonriente”.

La gran utilidad de las funciones unimodales es que se pueden calcular sus valores máximos y mínimos de forma mucho más eficiente que con una búsqueda lineal, algo que no es posible con una función cualquiera que suba y baje todo el tiempo de forma impredecible.

Un ejemplo muy simple de función unimodal sonriente sería el siguiente:

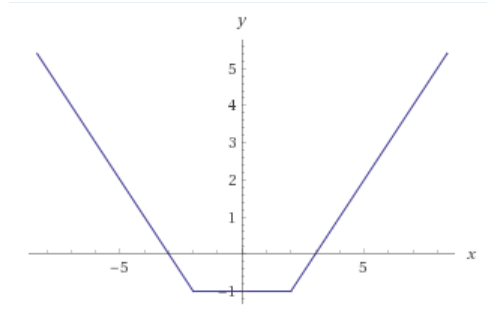
Esta función muy sencilla tiene tres partes, y la función es una recta en cada una: primero baja, luego es horizontal, luego sube, cumpliendo perfectamente lo necesario para ser una función unimodal sonriente.

Otro ejemplo podría ser el siguiente:

En este ejemplo la diferencia entre las partes no es tan evidente en el dibujo, pero se ve que se produce un cambio en el máximo: Allí, la función venía siendo estrictamente creciente, y pasa a ser estrictamente decreciente. En este ejemplo, la parte “constante” del medio tiene longitud $0$. Esto no es un problema, y la función sigue siendo unimodal: lo importante es que, si hay tramos constantes donde ni sube ni baja, estos deben estar todos juntos en el medio, y no en cualquier lugar, o la función no es unimodal. Esta función es unimodal triste.

Los dos ejemplos anteriores fueron funciones convexas y cóncavas respectivamente. Sin embargo, esto no tiene por qué ser así, y hay funciones unimodales que no son ni cóncavas ni convexas. Un ejemplo es la función $f$ dada por $f(x) = x^4 - 2x^2 - 4x$, cuyo gráfico se muestra a continuación:

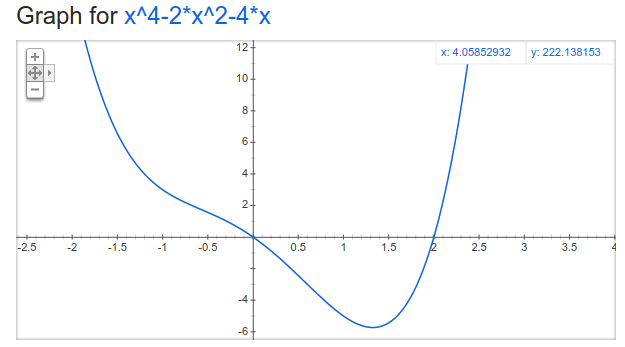
Se puede ver que si bien la función parece “zigzaguear” un poco en su descenso, siempre sigue siendo estrictamente decreciente hasta llegar al valor mínimo, y a partir de allí es siempre estrictamente creciente²⁾. Por lo tanto, esta función es unimodal sonriente, aunque no es convexa.

• El máximo de varias funciones unimodales sonrientes, es también una función unimodal sonriente. Es falso con unimodales tristes.
• El mínimo de varias funciones unimodales tristes, es también una función unimodal triste. Es falso con unimodales sonrientes.
• Una función $f$ es convexa si y solo si $-f$ es cóncava.
• Una función $f$ es unimodal sonriente si y solo si $-f$ es unimodal triste.
• Una función convexa también es automáticamente unimodal sonriente. (Convexa es una condición más fuerte, y las convexas son un tipo especial de unimodales sonrientes).
• Una función cóncava también es automáticamente unimodal triste. (Cóncava es una condición más fuerte, y las cóncavas son un tipo especial de unimodales tristes).
• Las funciones lineales son las únicas que son al mismo tiempo convexas y cóncavas.
• Las funciones estrictamente decrecientes, las estrictamente crecientes y las constantes (una recta horizontal) son las únicas que son al mismo tiempo unimodales tristes y unimodales sonrientes.
• Tanto la suma como el máximo de varias funciones convexas, es a su vez una función convexa.
• Tanto la suma como el mínimo de varias funciones cóncavas, es a su vez una función cóncava.
• CUIDADO: Una suma de funciones unimodales (incluso del mismo tipo) no tiene por qué ser unimodal, a menos que sepamos que además de unimodales también son funciones cóncavas/convexas.

Notar que de las anteriores surgen dos “recetas muy comunes” que producen siempre funciones unimodales:

• Si partimos de funciones lineales y solo sumamos y tomamos máximos, terminamos con una función convexa, y por lo tanto unimodal sonriente (Haciendo sumas y tomando mínimos, tendremos una cóncava).
• Si partimos de funciones monótonas o constantes, y solamente tomamos máximos, terminamos con una función unimodal sonriente (si solamente tomamos mínimos, terminamos con una unimodal triste).

Al final de este artículo se encuentran las ideas para demostrar estas propiedades útiles.

Ya adelantamos antes que lo bueno de las funciones unimodales es que se puede calcular su máximo y su mínimo eficientemente. El caso más fácil es el de calcular el máximo de una función unimodal sonriente: Se puede observar sobre el dibujo de estas funciones, que el máximo necesariamente se encuentra en un extremo, es decir, o bien está en el mínimo valor posible de $x$, o bien está en el máximo valor posible de $x$³⁾. Esto porque, sobre la parte “decreciente”, que es la que viene al principio, el mejor valor está justamente al comienzo de todo. Y sobre la parte “creciente”, que viene al final, el mejor valor está justamente al final de todo. Si hubiera una parte constante en el medio, no aporta nada nuevo, pues su valor es igual a los mínimos de las partes creciente y decreciente ya analizadas.

Lo mismo ocurre si buscamos el mínimo de una función unimodal triste: Necesariamente tiene que estar en uno de los dos extremos.

Por esta razón, es muy simple encontrar el máximo/mínimo en estos casos: Evaluamos la función en los dos extremos, y nos quedamos con el máximo/mínimo que nos interesa.

Nos falta ver el caso interesante. Nos concentraremos por simplicidad solamente en el cálculo del mínimo en una función unimodal sonriente, ya que el otro es idéntico intercambiando la dirección de todas las comparaciones⁴⁾.

Supondremos a continuación el caso más común en programación competitiva, que es aquel en que tanto el dominio como la imagen de la función toman valores enteros. Es decir, $f$ toma solamente enteros, y dado un entero $x$, el resultado $f(x)$ es también entero.

Recordemos el dibujo de una función unimodal sonriente:

Lo que caracteriza a estas funciones es que primero decrecen estrictamente, luego pueden mantenerse constantes un rato, y finalmente crecen estrictamente. De todo esto, se observa que siempre el valor mínimo se encuentra “en el medio”, y es exactamente el valor que toma la función en el tramo constante. Este tramo constante podría tener longitud $0$, y el mínimo darse en un solo punto, pero siempre es allí, en este tramo “central” de los 3 en que está dividida una función unimodal, en que se encuentra el mínimo.

Pensemos entonces en la comparación entre $f(x)$ y $f(x+1)$. ¿Cuál es más grande entre ellos? En una función cualquiera, la respuesta va cambiando todo el tiempo caóticamente, pero en una función unimodal eso solo cambia al “cruzar” entre partes: En la primera parte decreciente, siempre es $f(x) > f(x+1)$. En la parte del medio, siempre es $f(x) = f(x+1)$. Y en la parte del final, siempre es $f(x) < f(x+1)$.

De lo que ya hemos dicho, se ve entonces en los dibujos que el primer valor de $x$ en el que $f(x) < f(x+1)$ tiene que ser necesariamente el último valor del tramo “constante”, donde la función está a punto de comenzar a subir. Por lo tanto, ese valor de $x$ es donde se alcanza el mínimo valor de $f(x)$.

¿Y cómo podemos hacer para encontrar ese primer valor de $x$ eficientemente? La clave está en observar que la propiedad de que $f(x) < f(x+1)$ es una propiedad binaria: No bien un cierto $x$ la cumpla, como el siguiente valor $f(x+1)$ es más grande, eso ya nos muestra que estamos en la “tercera parte” de la unimodal, en la parte creciente: Por lo tanto, la función a partir de ahí siempre sigue creciendo, y entonces todos los $x$ siguientes también cumplirán la propiedad de que $f(x) < f(x+1)$. Podemos entonces usar búsqueda binaria para encontrar este primer $x$, y entonces sabremos que $f(x)$ es el mínimo valor de la función⁵⁾.

El código, siguiendo la receta, quedaría así:

   int a = a_inicial; // Tiene que ser f(a) >= f(a+1), para que sea uno que NO cumple la propiedad.
   int b = b_inicial; // Tiene que ser f(b)  < f(b+1), para que sea uno que SI cumple la propiedad.
   while (b-a > 1)
   {
       int c = (a+b)/2;
       if (f(c) < f(c+1))
          b = c;
       else
          a = c;
   }
   // b es el primero que cumple, y por lo tanto f(b) es el minimo valor de f
   return f(b);

Existe otro algoritmo diferente, también eficiente⁶⁾ y que se puede aplicar en estos casos en lugar de la búsqueda binaria que acabamos de mostrar, y es el de búsqueda ternaria.

Esta búsqueda tiene la misma idea principal que la búsqueda binaria, que es la idea de ir examinando valores de la función y “descartando” posiciones candidatas en base a la información obtenida.

En cada paso, tendremos entonces dos extremos $a$ y $b$, y lo que sabemos en todo momento es que el mínimo que estamos buscando está dentro de este intervalo. Es decir, una posición con el valor mínimo que buscamos se encuentra seguro en $[a,b)$. Al final, cuando tengamos $b=a+1$, es decir, cuando tengamos un intervalo de longitud $1$, habremos localizado el mínimo.

La gran diferencia está en que búsqueda binaria en cada paso examina la situación en la posición central, separando todo el intervalo que estamos analizando en dos partes. La búsqueda ternaria, como sugiere su nombre, separa el intervalo en tres partes, y para ello examina el valor de la función en los dos puntos de división entre las partes.

Es decir, vamos a examinar dos posiciones dentro de nuestro intervalo, $m_1$ y $m_2$, con $a \leq m_1<m_2 < b$.

Si $f(m_1) \leq f(m_2) $, sabemos que necesariamente $m_2$ ya pasó la primera parte inicial, en la que la función decrece estrictamente: si no fuera así, la función decrecería siempre estrictamente entre $m_1$ y $m_2$, y sería imposible observar lo que estamos observando. Por lo tanto, como el valor mínimo que buscamos se puede encontrar siempre en el último punto de la parte decreciente⁷⁾, y este está más a la izquierda que $m_2$, asignaremos $b = m_2$. Observemos que no podemos asignar $b$ a nada más pequeño con seguridad: podría ser que el mínimo estuviera de hecho en $m_2-1$, y que la razón por la que vemos que $f(m_1) < f(m_2)$ fuera que la función tenga un aumento enooooooooorme entre $m_2-1$ y $m_2$, que supere todo lo que venía bajando desde $m_1$ hasta $m_2-1$.

Si $f(m_1) > f(m_2) $, con un razonamiento análogo podemos deducir que $m_1$ está todavía estrictamente dentro de la primera parte, en la que la función está decreciendo estrictamente (pues sino, la función nunca decrecería entre $m_1$ y $m_2$), y entonces podemos poner $a = m_1+1$, ya que el mínimo tiene que estar sí o sí más a la derecha que $m_1$. No podemos poner $a$ en nada más grande, ya que podría pasar que el máximo esté en efecto en $m_1+1$: por ejemplo, eso ocurriría si la razón por la que es $f(m_1) > f(m_2)$ fuera que la función tiene un enooooooorme decrecimiento entre $m_1$ y $m_1+1$, que compense lo que luego sube desde $m_1+1$ hasta $m_2$.

Para elegir $m_1$ y $m_2$, partimos al intervalo $[a,b)$ en tres, tomando:

• $m_1=a+\left \lfloor \frac{b-a}{3} \right \rfloor$
• $m_2=a+\left \lfloor \frac{2(b-a)}{3} \right \rfloor$

Si $b-a>1$, estos dos valores $m_1$ y $m_2$ son siempre distintos entre sí, y caen dentro del rango $[a,b)$. Además, estando $m_1$ y $m_2$ dentro del rango, los reemplazos $a=m_1+1$ y $b=m_2$ siempre achican el rango, así que el procedimiento va a llegar en algún momento a tener un rango de un único elemento⁸⁾, que será el mínimo.

El código quedaría entonces:

   // Los valores iniciales deben ser tales que haya un minimo en el rango [a,b) inicial.
   int a = a_inicial;
   int b = b_inicial;
   while (b-a>1)
   {
      int m1 = a + (b-a)/3;
      int m2 = a + (2*(b-a))/3;
      if (f(m1) <= f(m2))
         b = m2;
      else
         a = m1+1;
   }
   return f(a); // El minimo esta en [a,a+1), o sea en a.

Polo the Penguin and Matrix

Dada una matriz de $n$ x $m$, una movida consiste en sumar o restar el número $d$ a una casilla que elijamos. Determinar la menor cantidad de movidas necesarias para hacer que todos los números sean iguales. Si es imposible, imprimir $-1$.

Para empezar, podemos ver con un poco de matemática, que al sumar o restar $d$ a un número, su resto en la división por $d$ no cambia. Luego, será posible alcanzar el objetivo si y sólo si todos los números tienen el mismo resto en la división por $d$.

Veamos cómo llevar este problema a buscar un mínimo en una función unimodal, para aplicar las técnicas que aprendimos.

Veamos que llevar todos los números a un número muy chiquito, puede llevarnos muchos pasos para mover los números grandes. Lo mismo si queremos llevar todos a un número muy grande, los chiquitos deberían sumar $d$ muchas veces. Es posible demostrar que esta función, que para cada posible número $x$ objetivo al cual queremos llevar los demás, nos dice la cantidad de pasos $f(x)$ necesarios, es una función unimodal sonriente: La razón es que la cantidad de pasos para una casilla particular es $\frac{|v_{casilla} - x|}{d}$, que como función de $x$ es convexa (ya que es la función valor absoluto trasladada y escalada), luego el costo total que es la suma de todas las casillas es suma de funciones convexas, y resulta también función convexa.

Entonces, buscaremos un número “intermedio” para el cual sea óptimo llevar a todos los números hacia éste, por lo tanto, con las técnicas que vimos para buscar mínimo de funciones unimodales sonrientes. Usaremos en este caso búsqueda ternaria, pero podríamos haber utilizado búsqueda binaria perfectamente.

Primero hay que ver cómo calcular la cantidad de movidas necesarias para llevar a todos los números a un número $v$, ya que eso es lo que nos permite evaluar $f(x)$ teniendo el $x$. Para eso, recorremos todos los números de la matriz, y la cantidad de movidas necesarias para cada número $a$ será la diferencia entre $a$ y $v$, dividido por $d$ que es cuánto se achica esa diferencia en cada movida; es decir, $abs(a-v)/d$.

Sabemos que el menor valor al que intentaremos llevar a todos los números será el valor más chico de la matriz, ya que si llevamos todo a $min-d$ por ejemplo, vamos a pasar por $min$ para todos los números, entonces nos conviene quedarnos ahí y nos llevará más pasos. Lo mismo para el mayor valor.

Hay que tener cuidado porque cuando hagamos (b-a)/3, quizás no caemos en un número de igual resto en la división por $3$ que lo que queremos, entonces pensar en llevar a todos los número hacia éste no tendría sentido. Lo que podemos hacer en este problema para evitar esto, es primero, restarles a todos los números su resto en la división por $d$, total lo que importa son sus diferencias relativas ya que vamos a sumar y restar $d$. Y luego, es pensar “a qué múltiplo de $d$ queremos llevar a todos los números”. Otra manera también sería divir todo por $d$ y pensar que las movidas suman y restan $1$, es completamente equivalente.

Otra manera diferente de razonar y resolver este problema se explica en este artículo.

solucion-con-ternaria.cpp

#include<bits/stdc++.h>
 
using namespace std;
 
#define forn(i,n) for(int i=0; i<(int)(n); i++)
 
int obtenerMovidas(vector<vector<int> > & matriz, int m, int d){
    int total = 0;
    forn(i, matriz.size()){
        forn(j, matriz[i].size()){
            total+=abs(matriz[i][j]-m)/d;
        }
    }
    return total;
}
 
int main(){
    int n, m, d;
    cin>>n>>m>>d;
    vector< vector<int> > matriz(n, vector<int>(m));
    int restoD;
    bool esPosible=true;
    int minimo=10002, maximo=0;
    forn(i, n){
        forn(j, m){
            cin>>matriz[i][j];
            if(i==0 and j==0){
                restoD=matriz[i][j]%d;
            }else{
                if(restoD!=matriz[i][j]%d){
                    esPosible=false;
                }
            }
            matriz[i][j]-=(matriz[i][j]%d);
            minimo=min(minimo, matriz[i][j]);
            maximo=max(maximo, matriz[i][j]);
        }
    }
    if(esPosible){
        // El minimo seguro esta en el rango [a,b) elegido
        int a=minimo/d, b=maximo/d + 1;
        #define costo(x) obtenerMovidas(matriz, (x)*d, d)
        while (b-a>1)
        {
            int m1 = a + (b-a)/3;
            int m2 = a + (2*(b-a))/3;
            if (costo(m1) <= costo(m2))
                b = m2;
            else
                a = m1+1;
        }
        // El optimo se encuentra en a, pues el rango es [a,a+1)
        cout << costo(a) << endl;
    }else{
        cout << -1 << endl;
    }
}

ternary search en Codeforces

Si podríamos haber usado búsqueda binaria común sin ningún problema en lugar de búsqueda ternaria, que es bastante más rebuscada ¿Cuál es el sentido de aprender a utilizar este método?

Una primera ventaja es conocer otro algoritmo, ya que siempre mientras más ideas aprendemos, más herramientas tenemos para crear nuestras propias ideas en otros problemas, basándonos en ideas que vimos en otros algoritmos anteriores.

Sin embargo, la ventaja auténtica de la búsqueda ternaria a la hora de buscar extremos de funciones unimodales, se observa en problemas con resultados inexactos, es decir con cómputos de punto flotante. Al trabajar con doubles y una función “continua” en los reales, no podemos hablar de “el siguiente real”, para verificar en un punto particular si la función está creciendo o decreciendo (que es lo que analizamos al comparar $f(x)$ y $f(x+1)$). Podríamos comparar $f(x)$ con $f(x+\epsilon)$, siendo $\epsilon$ un valor muy chiquito, pero esto es propenso a errores de precisión en los cálculos y puede llevar a resultados erróneos, ya que estaríamos haciendo una comparación crítica en el algoritmo de dos valores muy muy cercanos.

En estos casos, la búsqueda ternaria resuelve ambos inconvenientes: Es mucho más numéricamente estable al operar con resultados de punto flotante, ya que se evalúa la función en valores más espaciados, lo que hace que pequeñas diferencias no sean tan críticas al algoritmo. Y no hay que andar pensando en “el siguiente real”, ya que no se evalúan “diferencias con el siguiente”, sino que simplemente se examina el valor de la función en $a + \frac{b-a}{3}$ y $a + \frac{2(b-a)}{3}$.

Al igual que pasaba con la búsqueda binaria, al utilizar la búsqueda ternaria en cómputos de punto flotante, podemos detener la búsqueda cuando el rango $[a,b)$ que sabemos que contiene al mínimo sea suficientemente pequeño, aceptando el error resultante.

   // Los valores iniciales deben ser tales que haya un minimo en el rango [a,b) inicial.
   const double EPS = 1e-9; // Determina el error que aceptamos, que impacta en la cantidad de pasos
   double a = a_inicial;
   double b = b_inicial;
   while (b-a>EPS)
   {
      int m1 = a + (b-a)/3.0;
      int m2 = a + (2.0*(b-a))/3.0;
      if (f(m1) <= f(m2))
         b = m2;
      else
         a = m1; // Ya no hay "+1": No hay un "siguiente numero real", es un continuo.
   }
   // Sabemos que el minimo esta en [a,b), asi que tomamos el punto medio como valor de compromiso.
   double x = (a+b)/2.0;
   return f(x);

: ¡Escribir unas demos!