Un árbol generador de un grafo, es un subgrafo conexo del mismo, que contiene a todos los vértices y es un árbol. Estas propiedades son equivalente a decir que es un árbol que contiene todos los nodos del grafo en cuestión, y a partir del cual se puede llegar al grafo agregando aristas.

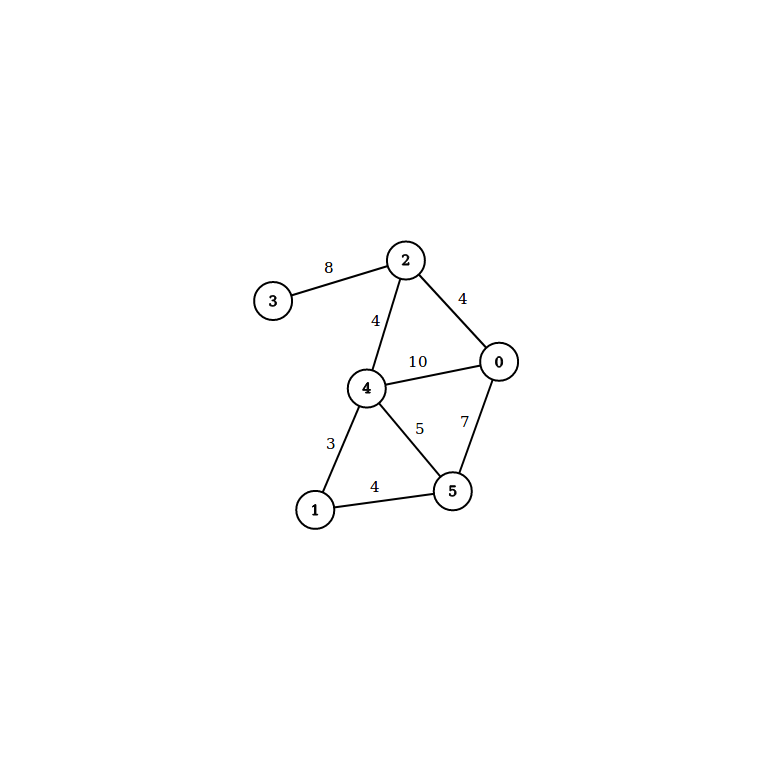
Por ejemplo:

$\rightarrow$

El árbol generador mínimo (AGM, o “MST” por sus siglas en inglés) de un grafo con aristas con pesos, es el grafo generador cuya suma de las aristas del árbol es mínimo dentro de todas las sumas de aristas de árboles generadores. En el caso de arriba, sería:

Hay dos algoritmos conocidos para encontrar el AGM: el de Prim y el de Kruskal.

Voy a contar la idea básica de ambos, sin detallar las demostraciones. Para conocerlas bien, pueden ver el link de wikipedia de Prim y Kruskal.

Idea: Inicializar un árbol con un solo nodo, cualquiera. Ir agregando de a un eje: Agrego el eje más chico de todos los que unen al árbol con nodos que no están todavía en el árbol.

Ejemplo con el grafo de arriba: Supongamos que agarramos el nodo $4$ como el árbol inicial. De todas las aristas que conectan al $4$ con otros nodos, la de valor más bajo es la arista de valor $3$, que une al $4$ con el $1$. Luego, podemos elegir la arista $(4,2)$ ó la arista $(1,5)$, ambas de valor $4$. Supongamos que agregamos la arista $(1,5)$ (es indistinto, con cualquier de las dos funciona igual). Ahora sí, la arista de valor más bajo que conecta a alguno de los nodos $4,1,5$ con los otros, es la arista $(4,2)$, de valor $4$. Entonces en nuestro árbol están los nodos $4,1,5,2$. Luego, agregamos al nodo $0$ mediante la arista $(2,0)$ de valor $4$. Y por último, el $3$ no está en el árbol, por lo que debo agregar la arista $(2,3)$. Finalmente termino con el AGM de la imagen anterior.

Este algoritmo, se puede ver como similar al algoritmo de Dijkstra, sólo que en vez de agarrar el nodo no recorrido de distancia más chica, agarramos el nodo fuera del árbol de distancia al árbol más chica.

#include<bits/stdc++.h>
 
using namespace std;
 
#define forn(i,n) for(int i=0; i<(int)(n); i++)
 
int main(){
    int n, m; // ingreso cantidad de nodos y de aristas
    cin>>n>>m;
    vector< vector< pair<int,int> > > grafo(n);
    map< pair<int,int>, int> longitudArista;
    forn(i, m){
        int u, v, longitud;
        cin>>u>>v>>longitud;
        grafo[u].push_back(make_pair(longitud, v));
        grafo[v].push_back(make_pair(longitud, u));
        longitudArista[make_pair(u,v)] = longitud;
        longitudArista[make_pair(v,u)] = longitud; // Guardamos esto para poder obtener la longitud dados los vértices
    }
    priority_queue< pair<int,int>, vector < pair<int,int> > , greater< pair<int,int> > > pq;
    int INF=1e9;
 
    int src = 0; // Tomo el nodo 0 como source, puede ser cualquiera
    vector<int> key(n, INF);
    vector<int> parent(n, -1);
    vector<bool> enAGM(n, false);
    pq.push(make_pair(0, src));
    key[src] = 0;
    while (!pq.empty()){
        int u = pq.top().second;
        pq.pop();
        enAGM[u] = true; // Así como marcábamos el visitado en Dijkstra, ahora lo marcamos como que ya está en el AGM, para no generar ciclos
        forn(i, grafo[u].size()){
            int v = grafo[u][i].second;
            int weight = grafo[u][i].first;
            if (enAGM[v] == false && key[v] > weight){ // Si ahora el nodo v está más cerca que lo que teníamos antes, actualizamos el valor en la priority_queue
                key[v] = weight;
                pq.push(make_pair(key[v], v));
                parent[v] = u; // Al actualizar, también marcamos que el mejor camino para llegar a v es desde u
            }
        }
    }
    int tamanioAGM = 0;
    forn(i, n){
	if(i!=src){ // El parent del src queda en -1 porque nunca lo actualizamos, enAGM[src] vale true desde el principio
		cout<<i<<" "<<parent[i]<<endl;
		tamanioAGM+=longitudArista[make_pair(i, parent[i])]; // Para esto guardamos la información en el mapa
	}
    }
    cout<<"Tamanio minimo = "<<tamanioAGM<<endl;
}

$\large O(E*log(V)$ ? Por qué?

Prerrequisitos: Estructura Union Find

Idea: La idea es, ordenar las aristas de menor valor a mayor, e ir agregando desde las más chicas, las que pueda sin que se genere un ciclo. La diferencia con Prim es que en Prim tenés siempre un árbol, y agregás de a un nodo al árbol. Acá, podés tener varios arbolitos separados, que de repente agregás una arista y unís dos árboles en uno. Esta oración es copada para entender el uso de Union Find. Empezamos con todos nodos separados, y vamos agregando aristas que conecten dos árboles diferentes, es decir que pertenezcan a distintos grupitos de nodos.

Ejemplo con el grafo de arriba: Primero ponemos la arista $(1, 4)$, de valor $3$. Luego, por ejemplo, la arista $(2,0)$, de valor $4$. Es lo mismo cómo ordenamos las de mismo valor. Quizás obtenemos un AGM distinto pero seguro va a tener el mismo valor total. Acá se ve que tenemos por un lado el grupito $\{0, 2\}$ y por otro el $\{1, 4\}$. Además de los grupitos de nodos aislados $\{3\}$ y $\{5\}$. Luego, agregamos por ejemplo la arista $(2,4)$ de valor $4$. Luego $(4,5)$ de valor $4$. Ahora, la arista de menor valor que deberíamos recorrer es $(4,5)$, de valor $5$. Pero eso nos genera un ciclo. O hablando en términos de union-find, los nodos $4$ y $5$ tiene el mismo representante, ya están unidos. Entonces no la agregamos. Tampoco la arista $(4,0)$ de valor $7$. Y por último, agregamos la arista $(3,2)$ de valor $8$, ya que el $3$ era un grupito aislado del resto. Terminamos, ya que agregamos $5$ aristas y hay $6$ nodos. Tenemos el mismo AGM que nos dio Prim y que está ilustrado más arriba. (En este ejemplo, el AGM es único.)

Este código, en mi opinión, es más lindo de implementar que Kruskal. Más allá de que requiera de la estructura Union-Find, el código queda simplemente “ordenar aristas; recorrer; if(tienen distintos represantes) entonces mergear nodos”.

#include<bits/stdc++.h>
 
using namespace std;
 
#define forn(i,n) for(int i=0; i<(int)(n); i++)
 
vector<int> padre, altura;
 
void init(int n){
	forn(i, n){
		padre.push_back(i);
		altura.push_back(1);
	}
}
 
int find(int x){
	if(padre[x]!=x){
		padre[x]=find(padre[x]);
	}
	return padre[x];
}
 
void merge(int x, int y){
	int px=find(x), py=find(y);
	if(altura[px]<altura[py]){
		padre[px]=py;
	}else{
		padre[py]=px;
		if(altura[px]==altura[py]){
			altura[px]++;
		}
	}
}
 
bool connected(int u, int v){
    return find(u)==find(v);
}
 
struct arista{
    int u, v, longitud;
};
 
bool compareAristas(arista a, arista b){
    return a.longitud<b.longitud;
}
 
int main(){
    int n, m; // ingreso cantidad de nodos y de aristas
    cin>>n>>m;
    // inicializo los n Disjoin-Sets que tienen como padre a sí mismos y tamanio 1.
    init(n);
    vector< arista > aristas;
    forn(i, m){
        arista a;
        cin>>a.u>>a.v>>a.longitud;
        aristas.push_back(a);
    }
    sort(aristas.begin(), aristas.end(), compareAristas);
    vector<arista> elegidas;
    int pesoMinimo=0;
    forn(i, m){
        arista a = aristas[i];
        if(!connected(a.u, a.v)){
            merge(a.u, a.v);
            elegidas.push_back(a);
            pesoMinimo+=a.longitud;
        }
    }
    cout<<"Peso minimo: "<<pesoMinimo<<endl;
    forn(i, n-1){
        cout<<elegidas[i].u<<" "<<elegidas[i].v<<endl;
    }
}

Se puede probar con el grafo del ejemplo, y se puede cambiar la función “compareAristas” para que si tienen misma longitud priorize la de menor $u$, o la de mayor $u$, para ver qué árbol elige (en un grafo con más de un AGM, por ejemplo se puede cambiar la longitud de la arista $(4, 5)$ de $5$ a $4$) y ver que el peso sigue siendo el mismo.

El algoritmo ordena las aristas, y luego las recorre y hace un par de finds y quizás un merge, que tienen complejidad muy baja, por lo que la complejidad del algoritmo termina siendo de $\large O(E*log(E))$