Herramientas de usuario
¡Esta es una revisión vieja del documento!
Tabla de Contenidos
Búsqueda binaria separadora
Situación
La búsqueda binaria “común” sirve para encontrar el “corte” en una propiedad binaria. Es decir, si tenemos una función $f$ monótona, que a cada entero le asigna un valor binario $0$ o $1$, búsqueda binaria sirve para encontrar el primer 1.
La situación que sea plantea aquí corresponde a encontrar los hasta $K-1$ posibles “cortes” de una función $K$-aria, es decir, que toma valores enteros en el rango $[0,K)$. Una manera de dar los cortes sería por ejemplo, dar el menor valor de $x$ tal que $f(x) \geq 1$, el menor valor de $x$ tal que $f(x) \geq 2$, y así hasta $K-1$, que es el máximo posible.
Solución trivial
Siempre podemos recorrer todos los $N$ valores de $x$ para buscar en una pasada todos los $K$ puntos de corte. Esto toma $O(N)$ evaluaciones de la función.
En adelante, asumiremos siempre que $N$, la cantidad posible de valores de $x$, es bastante mayor que $K$, pues sino no hay nada considerablemente mejor que este barrido exhaustivo.
Solución razonable
Una solución razonable para este problema es utilizar búsqueda binaria para encontrar cada uno de los cortes, de manera totalmente independiente. Es decir, se ejecutaría $K-1$ veces el algoritmo usual de búsqueda binaria sobre todo el rango posible de $N$ valores: Una para buscar el corte de los $1$, otra para el corte de los $2$, y así siguiendo. Cada una es una consulta usual de lower_bound, con su correspondiente valor.
Como cada búsqueda binaria tiene un costo $O(\ļg N$)$, el costo total en peor caso es $O(K \lg N)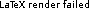 x$ tal que $f(x) = 1$, necesariamente el primer $2$ deberá estar después, así que podemos tomar como inicio del rango de la búsqueda binaria este valor de $x
x$ tal que $f(x) = 1$, necesariamente el primer $2$ deberá estar después, así que podemos tomar como inicio del rango de la búsqueda binaria este valor de $x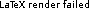 \lg N
\lg N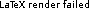 a$ es la posición "base" donde encontramos el corte anterior (de modo que sabemos que el corte de este paso está más adelante), comenzamos evaluando $f$ en las posiciones $a+1$, $a+2$, $a+4$, $a+8$, $a+16$, y así siguiendo hasta que alguna cumpla $f(x) \geq t$, siendo $t
a$ es la posición "base" donde encontramos el corte anterior (de modo que sabemos que el corte de este paso está más adelante), comenzamos evaluando $f$ en las posiciones $a+1$, $a+2$, $a+4$, $a+8$, $a+16$, y así siguiendo hasta que alguna cumpla $f(x) \geq t$, siendo $t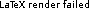 f(a+8) < t$, pero $f(a+16) \geq t$, descubrimos que el corte está entre $a+8$ y $a+16
f(a+8) < t$, pero $f(a+16) \geq t$, descubrimos que el corte está entre $a+8$ y $a+16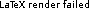 f(x) \geq t$ con este método es $O(\lg(x_t - x_{t-1}))
f(x) \geq t$ con este método es $O(\lg(x_t - x_{t-1}))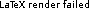 O(K \lg (\frac{N}{K}))$: el peor caso se da ahora cuando los cortes están bien distribuidos, de modo que las distancias entre ellos son aproximadamente iguales.
O(K \lg (\frac{N}{K}))$: el peor caso se da ahora cuando los cortes están bien distribuidos, de modo que las distancias entre ellos son aproximadamente iguales.
Solución eficiente: recursión
 : Presentar esta solución, que sería la mejor aunque no mejora la complejidad asintótica de la anterior.
: Presentar esta solución, que sería la mejor aunque no mejora la complejidad asintótica de la anterior.
Comparación de soluciones
 : Correr experimentos anecdóticos para mostrar que están ordenadas como aquí se presentan.
: Correr experimentos anecdóticos para mostrar que están ordenadas como aquí se presentan.
¿Por qué puede importar una diferencia tan pequeña en la complejidad?
Si bien el impacto en el tiempo de ejecución es pequeño, hay varias razones más allá de eso para que nos importe. Las más importantes son:
- Entender las ideas involucradas en estos algoritmos pueden permitir aplicar ideas similares en otras situaciones, donde la ganancia sea mucho mayor.
- En problemas interactivos (muy comunes por ejemplo en IOI), es posible para el sistema corrector medir exactamente la cantidad de llamadas a las funciones que utilizamos, y en estos casos es fácil (y común) forzar a optimizar la cantidad de llamadas, pues no hace falta medir tiempos para distinguir cuántas llamadas se usan. Por eso en estos problemas, podría ser que una de estas soluciones obtenga 100 puntos y otras no.
Problema de aplicación
 : Dejar link a “Prize”
: Dejar link a “Prize”

